Mica Dam Expansion Water Temperature and Fish Indexing Study 2020

2021-05-21

The suggested citation for this analytic appendix is:

Thorley, J.L. & Amies-Galonski, E. (2021) Mica Dam Expansion Water Temperature and Fish Indexing Study 2020. A Poisson Consulting Analysis Appendix. URL: https://www.poissonconsulting.ca/f/955630057.

Background

The Mica Tailrace Fish Indexing Study is a multi-year program to estimate the effects of the addition of two new turbines (Mica 5 and 6) on the ichyofauna and thermal regime in the 2.5 km of the Columbia River downstream of Mica Dam. A single year of fish indexing data (2008) was also available from a previous program. As per the Terms of Reference (TOR) the relative abundance, condition and spatial distribution of the fish populations was assessed.

Mica 5 became operational on January 28th 2015 and Mica 6 became operational on December 22nd 2015.

Data Preparation

The fish and downstream temperature data were provided by the Ktunaxa Nation. The discharge and elevation data were queried from the Columbia Basin Hydrological Database.

The data were cleaned and tidied using R version 4.0.5 (R Core Team 2020).

Length Cutoffs

Individuals were classified as fry (age-0), juvenile (age-1 and older subadults) or adult (sexually mature) based on the length cut-offs in Table 1.

Statistical Analysis

Model parameters were estimated using Bayesian methods. The estimates were produced using JAGS (Plummer 2003). For additional information on Bayesian estimation the reader is referred to McElreath (2016).

Unless stated otherwise, the Bayesian analyses used weakly informative normal and half-normal prior distributions (Gelman, Simpson, and Betancourt 2017). The posterior distributions were estimated from 1500 Markov Chain Monte Carlo (MCMC) samples thinned from the second halves of 3 chains (Kery and Schaub 2011, 38–40). Model convergence was confirmed by ensuring that the potential scale reduction factor \(\hat{R} \leq 1.05\) (Kery and Schaub 2011, 40) and the effective sample size (Brooks et al. 2011) \(\textrm{ESS} \geq 150\) for each of the monitored parameters (Kery and Schaub 2011, 61).

The parameters are summarised in terms of the point estimate, lower and upper 95% credible limits (CLs) and the surprisal s-value (Greenland 2019). The estimate is the median (50th percentile) of the MCMC samples while the 95% CLs are the 2.5th and 97.5th percentiles. The s-value can be considered a test of directionality. More specifically it indicates how surprising (in bits) it would be to discover that the true value of the parameter is in the opposite direction to the estimate. An s-value of 4.3 bits, which is equivalent to a p-value (Kery and Schaub 2011; Greenland and Poole 2013) of 0.05, indicates that the surprise would be equivalent to throwing 4.3 heads in a row. The requirement that non-essential explanatory variables have s-values \(\geq\) 4.3 bits provides a useful model selection heuristic (Kery and Schaub 2011).

The results are displayed graphically by plotting the modeled relationships between particular variables and the response(s) with the remaining variables held constant. In general, continuous and discrete fixed variables are held constant at their mean and first level values, respectively, while random variables are held constant at their typical values (expected values of the underlying hyperdistributions) (Kery and Schaub 2011, 77–82). When informative the influence of particular variables is expressed in terms of the effect size (i.e., percent or n-fold change in the response variable) with 95% credible intervals (CIs, Bradford, Korman, and Higgins 2005).

The analyses were implemented using R version 4.0.5 (R Core Team 2020) and the mbr family of packages.

Model Descriptions

Body Condition

The annual variation in condition (body weight when accounting for body length) was estimated from the boat and backpack electrofishing captures using a mass-length model (He et al. 2008).

Key assumptions of the condition model include:

  • Weight varies with body length as an allometric relationship, i.e., \(W = \alpha L^{\beta}\).
  • \(\alpha\) varies randomly with year.
  • \(\alpha\) varies by period (pre versus post Mica 5 and 6).
  • The residual variation in weight is log-normally distributed.

Preliminary analyses indicated that site and day of the year were not informative predictors of condition.

Relative Abundance

The annual variation in relative abundance was estimated from the boat count and catch data using an over-dispersed Poisson model (Kery and Schaub 2011). Lineal densities are by kilometre of river (as opposed to kilometre of bank).

Key assumptions of the relative abundance model include:

  • Lineal count density varies by period.
  • Lineal count density varies randomly with year.
  • Lineal catch efficiency is a fixed multiplier of lineal count efficiency.
  • Expected counts (and catches) are the product of the count (catch) density and the length of river (half the length of bank) sampled.
  • Observed counts (and catches) are described by a Poisson-gamma distribution.

Preliminary analyses indicated that site and discharge were not informative predictors of the lineal count (or catch) density.

The model does not distinguish between the abundance and observer efficiency, i.e., it estimates the count which is the product of the two. As such it is necessary to assume that changes in observer efficiency by year are negligible in order to interpret the estimates as relative abundance.

Water Temperature

Tailrace

Climatic variation can cause large differences in annual temperatures. Consequently, we explored the data for an effect of the additional turbines on the difference in the water temperature between the right versus left bank and when moving downstream. All apparent systematic differences were within the accuracy of the temperature loggers (\(\pm 0.2^{\circ}\text{C}\)).

Forebay and Tailrace

In 2020 the BC Hydro thermistor data for the Mica Dam forebay were analysed using Maximum Likelihood (Millar 2011) and TMB (Kristensen et al. 2016) to determine the extent to which discharge from the turbines and the air temperature influences the water temperature in the tailrace.

Key assumptions of the hourly temperature model include:

  • The effective depth of each unit depends on the unit (as a random effect) and its discharge (as a fixed effect).
  • The water temperature effect of each unit depends on its effective depth and the stratification in the forebay.
  • The water temperature is affected by release from the dam and the difference in air temperature and the water temperature.
  • The temporal autocorrelation is described a first order moving average process.
  • The residual water temperature at the tailrace temperature logger is normally distributed.

Despite the incorporation of a first order moving average process the residual variation in the hourly tailrace water temperature was strongly autocorrelated. Consequently CIs are not provided for the coefficients or estimates.

Model Templates

Condition

.model{
  bAlpha ~ dnorm(5, 2^-2)
  bBeta ~ dnorm(3, 2^-2)

  bAlphaPeriod[1] <- 0
  for(i in 2:nPeriod) {
    bAlphaPeriod[i] ~ dnorm(0, 2^-2)
  }

  sAlphaAnnual ~ dnorm(0, 2^-2) T(0,)
  for(i in 1:nAnnual) {
    bAlphaAnnual[i] ~ dnorm(0, sAlphaAnnual^-2)
  }

  sWeight ~ dnorm(0, 2^-2) T(0,)
  for (i in 1:length(Weight)) {
    eAlpha[i] <- bAlpha + bAlphaPeriod[Period[i]] + bAlphaAnnual[Annual[i]]
    eBeta[i] <- bBeta
    log(eWeight[i]) <- eAlpha[i] + eBeta[i] * Length[i]
    Weight[i] ~ dlnorm(log(eWeight[i]), sWeight^-2)
  }

Block 1.

Relative Abundance

.model{
  bEfficiencyVisitType[1] <- 0
  for (i in 2:nVisitType) {
    bEfficiencyVisitType[i] ~ dnorm(0, 1^-2)
  }

  bDensity ~ dnorm(0, 5^-2)

  bDensityPeriod[1] <- 0
  for(i in 2:nPeriod) {
    bDensityPeriod[i] ~ dnorm(0, 2^-2)
  }

  sDensityAnnual ~ dnorm(0, 2^-2) T(0, )
  for(i in 1:nAnnual) {
    bDensityAnnual[i] ~ dnorm(0, sDensityAnnual^-2)
  }

  sDispersion ~ dnorm(0, 2^-2) T(0, )
  for (i in 1:length(Annual)) {
    log(eEfficiency[i]) <- bEfficiencyVisitType[VisitType[i]]
    log(eDensity[i]) <- bDensity + bDensityPeriod[Period[i]] + bDensityAnnual[Annual[i]]
    eAbundance[i] <- eDensity[i] * SiteLength[i] / 2
    eDispersion[i] ~ dgamma(1 / sDispersion^2, 1 / sDispersion^2)
    Count[i] ~ dpois(eAbundance[i] * eEfficiency[i] * eDispersion[i])
  }

Block 2.

Forebay and Tailrace

.#include <TMB.hpp>

template<class Type>
Type objective_function<Type>::operator() () {

DATA_VECTOR(Tailrace);
DATA_VECTOR(Intake);
DATA_VECTOR(Forebay);
DATA_VECTOR(Air);
DATA_VECTOR(Unit1);
DATA_VECTOR(Unit2);
DATA_VECTOR(Unit3);
DATA_VECTOR(Unit4);
DATA_VECTOR(Unit5);
DATA_VECTOR(Unit6);
DATA_VECTOR(Spill);
DATA_IVECTOR(Consecutive);

PARAMETER(sDepthUnit);
PARAMETER_VECTOR(bDepthUnit);
PARAMETER(bDepthSpill0);
PARAMETER_VECTOR(bDepthTurbineUnit);
PARAMETER(bRelease);
PARAMETER(bReleaseAir);
PARAMETER(bRho);
PARAMETER(sTailrace);

vector<Type> eTurbineUnit1 = Tailrace;
vector<Type> eTurbineUnit2 = Tailrace;
vector<Type> eTurbineUnit3 = Tailrace;
vector<Type> eTurbineUnit4 = Tailrace;
vector<Type> eTurbineUnit5 = Tailrace;
vector<Type> eTurbineUnit6 = Tailrace;
vector<Type> eDischarge = Tailrace;
vector<Type> eDepthTurbineUnit1 = Tailrace;
vector<Type> eDepthTurbineUnit2 = Tailrace;
vector<Type> eDepthTurbineUnit3 = Tailrace;
vector<Type> eDepthTurbineUnit4 = Tailrace;
vector<Type> eDepthTurbineUnit5 = Tailrace;
vector<Type> eDepthTurbineUnit6 = Tailrace;
vector<Type> eDepthSpill = Tailrace;
vector<Type> eStratification = Tailrace;
vector<Type> eEffectTurbineUnit1 = Tailrace;
vector<Type> eEffectTurbineUnit2 = Tailrace;
vector<Type> eEffectTurbineUnit3 = Tailrace;
vector<Type> eEffectTurbineUnit4 = Tailrace;
vector<Type> eEffectTurbineUnit5 = Tailrace;
vector<Type> eEffectTurbineUnit6 = Tailrace;
vector<Type> eEffectSpill = Tailrace;
vector<Type> eEffectDischarge = Tailrace;
vector<Type> eReleaseEffect = Tailrace;
vector<Type> eOutput = Tailrace;
vector<Type> eRelease = Tailrace;
vector<Type> eTailrace = Tailrace;

Type nll = 0.0;

eTailrace(0) = Tailrace(0);

for(int i = 0; i < 6; i++){
  nll -= dnorm(bDepthUnit(i), Type(0), exp(sDepthUnit), true);

for(int i = 1; i < Tailrace.size(); i++){
  eTurbineUnit1(i) = Unit1(i) + 0.0001;
  eTurbineUnit2(i) = Unit2(i) + 0.0001;
  eTurbineUnit3(i) = Unit3(i) + 0.0001;
  eTurbineUnit4(i) = Unit4(i) + 0.0001;
  eTurbineUnit5(i) = Unit5(i) + 0.0001;
  eTurbineUnit6(i) = Unit6(i) + 0.0001;
  eDischarge(i) = eTurbineUnit1(i) + eTurbineUnit2(i) + eTurbineUnit3(i) + eTurbineUnit4(i) + eTurbineUnit5(i) + eTurbineUnit6(i) + Spill(i);
  eDepthTurbineUnit1(i) = bDepthUnit(0) + bDepthTurbineUnit(0) * eTurbineUnit1(i);
  eDepthTurbineUnit2(i) = bDepthUnit(1) + bDepthTurbineUnit(1) * eTurbineUnit2(i);
  eDepthTurbineUnit3(i) = bDepthUnit(2) + bDepthTurbineUnit(2) * eTurbineUnit3(i);
  eDepthTurbineUnit4(i) = bDepthUnit(3) + bDepthTurbineUnit(3) * eTurbineUnit4(i);
  eDepthTurbineUnit5(i) = bDepthUnit(4) + bDepthTurbineUnit(4) * eTurbineUnit5(i);
  eDepthTurbineUnit6(i) = bDepthUnit(5) + bDepthTurbineUnit(5) * eTurbineUnit6(i);
  eDepthSpill(i) = bDepthSpill0;
  eStratification(i) = (Forebay(i) - Intake(i)) / (707 - 690) ;
  eEffectTurbineUnit1(i) = eDepthTurbineUnit1(i) * eStratification(i);
  eEffectTurbineUnit2(i) = eDepthTurbineUnit2(i) * eStratification(i);
  eEffectTurbineUnit3(i) = eDepthTurbineUnit3(i) * eStratification(i);
  eEffectTurbineUnit4(i) = eDepthTurbineUnit4(i) * eStratification(i);
  eEffectTurbineUnit5(i) = eDepthTurbineUnit5(i) * eStratification(i);
  eEffectTurbineUnit6(i) = eDepthTurbineUnit6(i) * eStratification(i);
  eEffectSpill(i) = eDepthSpill(i) * eStratification(i);
  eEffectDischarge(i) = (eEffectTurbineUnit1(i) * eTurbineUnit1(i) + eEffectTurbineUnit2(i) * eTurbineUnit2(i) + eEffectTurbineUnit3(i) * eTurbineUnit3(i) + eEffectTurbineUnit4(i) * eTurbineUnit4(i) + eEffectTurbineUnit5(i) * eTurbineUnit5(i) + eEffectTurbineUnit6(i) * eTurbineUnit6(i) + eEffectSpill(i) * Spill(i)) / eDischarge(i);
  eReleaseEffect(i) = exp(bRelease + bReleaseAir * (Air(i) - Intake(i)));
  eOutput(i) = Intake(i) + eEffectDischarge(i);
  eRelease(i) = eOutput(i) + eReleaseEffect(i);
  eTailrace(i) = eRelease(i) + Consecutive(i) * invlogit(bRho) * (Tailrace(i-1) - eTailrace(i-1));
  nll -= dnorm(Tailrace(i), eTailrace(i), exp(sTailrace), true);
return nll;

Block 3. Model description.

Results

Tables

Table 1. Life-stage fork length cutoffs by species.

Species Fry Juvenile
Bull Trout 120 400
Kokanee 100 250
Mountain Whitefish 120 175
Rainbow Trout 120 250

Condition

Table 2. Parameter descriptions.

Parameter Description
Annual[i] Year of capture of ith fish as a factor
bAlpha Intercept for eAlpha
bAlphaAnnual[i] Effect of ith Annual on bAlpha
bAlphaPeriod[i] Effect of ith Period on bAlpha
bBeta Intercept for eBeta
eAlpha[i] Predicted allometric intercept (on centred log length) for ith fish
eBeta[i] Predicted allometric slope for ith fish
eWeight[i] Predicted Weight of ith fish
Length[i] Centred log Length of ith fish
Period[i] The second period is post Mica 5 and 6
sAlphaAnnual SD of bAlphaAnnual
sWeight SD of residual variation in log(Weight)
Weight[i] Weight of ith fish
Bull Trout

Table 3. Model coefficients.

term estimate lower upper svalue
bAlpha 6.8707736 6.5435297 7.1957171 10.551708
bAlphaPeriod[2] -0.1045242 -0.6302385 0.3420439 1.106693
bBeta 3.1078848 2.9812488 3.2404450 10.551708
sAlphaAnnual 0.1389986 0.0423917 0.6807784 10.551708
sWeight 0.1886779 0.1665397 0.2173000 10.551708

Table 4. Model summary.

n K nchains niters nthin ess rhat converged
107 5 3 500 1000 1174 1.004 TRUE
Mountain Whitefish

Table 5. Model coefficients.

term estimate lower upper svalue
bAlpha 5.2794527 5.1147382 5.4558767 10.5517083
bAlphaPeriod[2] -0.0521814 -0.3096497 0.2515648 0.9723923
bBeta 3.1365429 3.0971546 3.1780172 10.5517083
sAlphaAnnual 0.0893753 0.0339886 0.4660849 10.5517083
sWeight 0.1167718 0.1108145 0.1232494 10.5517083

Table 6. Model summary.

n K nchains niters nthin ess rhat converged
687 5 3 500 1000 500 1.008 TRUE
Kokanee

Table 7. Model coefficients.

term estimate lower upper svalue
bAlpha 4.7682144 4.5271276 5.1143568 10.5517083
bAlphaPeriod[2] 0.0402219 -0.4674362 0.4473064 0.3905764
bBeta 3.2836558 3.2152250 3.3545707 10.5517083
sAlphaAnnual 0.1480292 0.0502591 0.6328982 10.5517083
sWeight 0.2608798 0.2398431 0.2876929 10.5517083

Table 8. Model summary.

n K nchains niters nthin ess rhat converged
240 5 3 500 1000 1202 1.001 TRUE

Relative Abundance

Table 9. Parameter descriptions.

Parameter Description
Annual[i] Year of ith site visit
bDensity Intercept for log(eDensity)
bDensityAnnual[i] Effect of ith Annual on log(eDensity)
bEfficiencyVisitType[i] Value of log(eEfficiency) for ith VisitType
Count[i] Number of fish counted or captured on ith site visit
eAbundance[i] Predicted relative abundance for ith site visit
eDensity[i] Predicted relative lineal density for ith site visit
eDispersion[i] Predicted over-dispersion for ith site visit
eEfficiency[i] Predicted efficiency relative to counting for ith site visit
sDispersion SD of eDispersion
SiteLength[i] Length of bank surveyed on ith site visit
VisitType[i] Type of ith site visit, i.e., count versus catch
Bull Trout

Table 10. Model coefficients.

term estimate lower upper svalue
bDensity 2.4367987 1.8728905 3.0346808 10.5517083
bDensityPeriod[2] 0.1264751 -0.6351285 0.8097706 0.5931555
bEfficiencyVisitType[2] -0.7045251 -1.1770378 -0.2147932 7.0922766
sDensityAnnual 0.1971853 0.0080181 0.9352467 10.5517083
sDispersion 0.6007875 0.3949569 0.8514637 10.5517083

Table 11. Model summary.

n K nchains niters nthin ess rhat converged
57 5 3 500 500 1302 1.001 TRUE
Mountain Whitefish

Table 12. Model coefficients.

term estimate lower upper svalue
bDensity 5.6330267 4.0594520 6.776410 10.5517083
bDensityPeriod[2] -0.1703173 -1.6307918 2.116392 0.3434739
bEfficiencyVisitType[2] -1.5643612 -2.0686241 -1.030629 10.5517083
sDensityAnnual 0.8232030 0.3630214 2.172976 10.5517083
sDispersion 0.8269002 0.6811523 1.018479 10.5517083

Table 13. Model summary.

n K nchains niters nthin ess rhat converged
57 5 3 500 500 162 1.019 TRUE
Rainbow Trout

Table 14. Model coefficients.

term estimate lower upper svalue
bDensity 0.9679847 -1.3878449 2.665015 1.565866
bDensityPeriod[2] -1.0680493 -3.3710270 1.336873 1.430175
bEfficiencyVisitType[2] -2.6469189 -3.9097537 -1.313103 10.551708
sDensityAnnual 1.4395039 0.4600191 3.463163 10.551708
sDispersion 0.7985581 0.3044938 1.694853 10.551708

Table 15. Model summary.

n K nchains niters nthin ess rhat converged
57 5 3 500 500 1178 1 TRUE
Kokanee

Table 16. Model coefficients.

term estimate lower upper svalue
bDensity 4.1090603 2.4065678 5.474832 10.5517083
bDensityPeriod[2] -0.2584851 -2.1020164 1.578466 0.3855452
bEfficiencyVisitType[2] -1.1210518 -1.7879443 -0.497317 8.9667458
sDensityAnnual 0.9593140 0.3722623 2.560715 10.5517083
sDispersion 0.9486383 0.7594875 1.198962 10.5517083

Table 17. Model summary.

n K nchains niters nthin ess rhat converged
47 5 3 500 500 453 1.01 TRUE

Forebay and Tailrace

Table 18. Parameter descriptions.

Parameter Description
Air Mean daily air temperature at the Mica weather station (C)
bDepthSpill The effective depth of the spill relative to the intake elevation of 690 masl
bDepthTurbineUnit[i] The effect of discharge on the effective depth of the ith unit
bDepthUnit[i] The effective depth of the ith unit relative to the intake elevation of 690 masl
bRelease The effect of release on the water temperature
bReleaseAir The effect of the difference in the mean daily air temperature at the Mica weather station and the hourly water temperature at thermistor in the forebay at 690 masl on the bRelease
bRho The coefficient for the first order moving average process
Consecutive Indicator variable specifying whether the current hour is consecutive
Forebay Hourly water temperature at the thermistor in the forebay at 707 masl (C)
Intake Hourly water temperature at the thermistor in the forebay at 690 masl (C)
sDepthUnit The standard deviation for the variation in bDepthUnit
Spill Hourly spill (cms)
sTailrace The standard deviation for the residual variation in Tailrace
Tailrace Hourly water temperature in the tail race at 366.3L (C)
Unit1 Hourly discharge through the 1st unit (cms)
Unit2 Hourly discharge through the 2nd unit (cms)
Unit6 Hourly discharge through the 6th unit (cms)

Table 19. Model coefficients estimates. The confidence limits are not provided as they are considered unreliable due to the extensive autocorrelation in the data.

term estimate
bDepthSpill0 20.1744463
bDepthTurbineUnit[1] 0.0145087
bDepthTurbineUnit[2] 0.0228736
bDepthTurbineUnit[3] 0.0027475
bDepthTurbineUnit[4] 0.0039504
bDepthTurbineUnit[5] 0.0016820
bDepthTurbineUnit[6] 0.0001977
bDepthUnit[1] 10.3067047
bDepthUnit[2] 8.6034577
bDepthUnit[3] 9.6747688
bDepthUnit[4] 9.9977596
bDepthUnit[5] 9.2025899
bDepthUnit[6] 9.1161212
bRelease -1.1280293
bReleaseAir 0.1059494
bRho 1.9785438
sDepthUnit 2.3090611
sTailrace -1.0427099

Table 20. Model convergence.

n K logLik IC converged
54552 18 -20536.39 41108.79 TRUE

Figures

Discharge

figures/discharge/spill.png

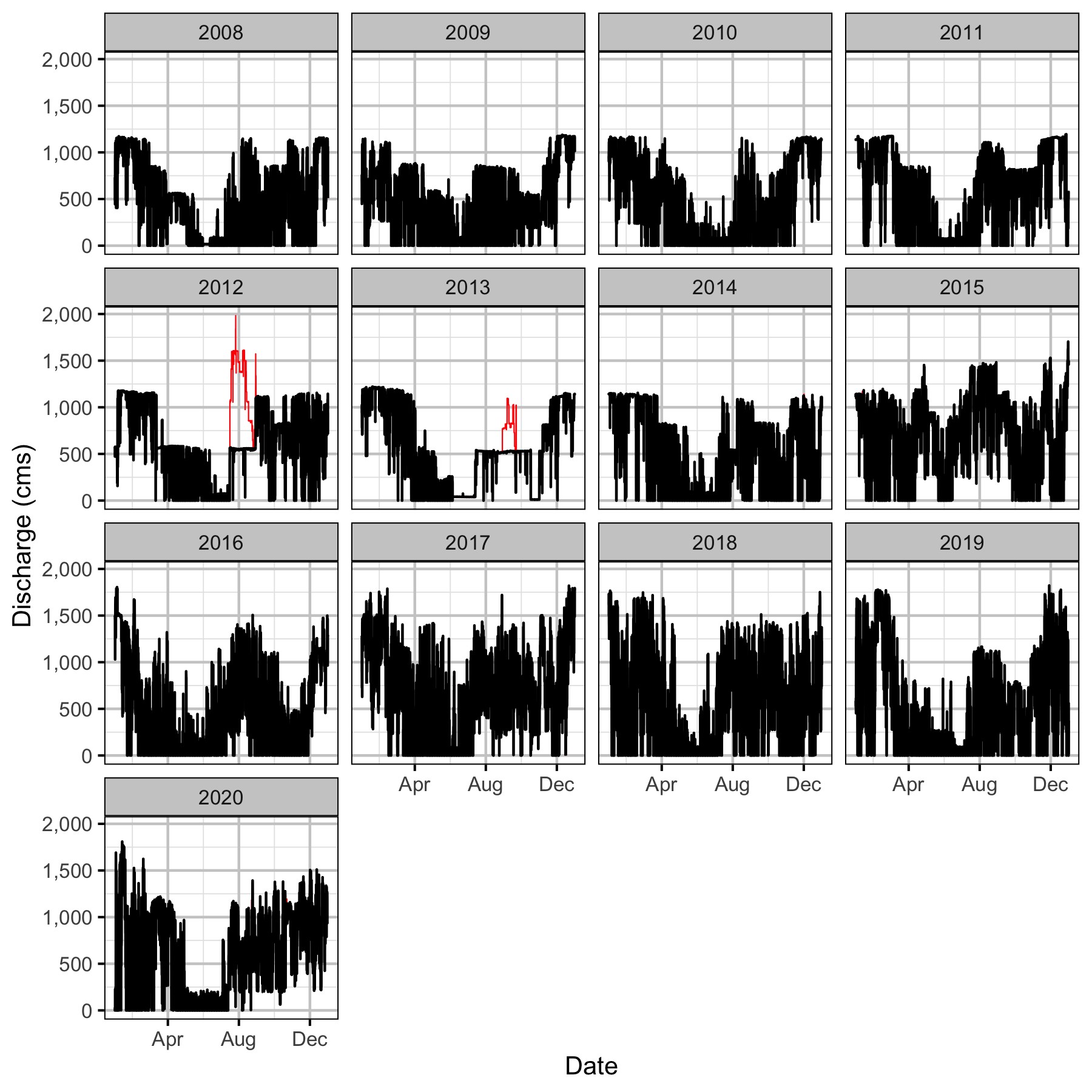
Figure 1. Hourly discharge from Mica Dam by turbines (black) and turbines plus spill (red).

figures/discharge/boat-visit.png

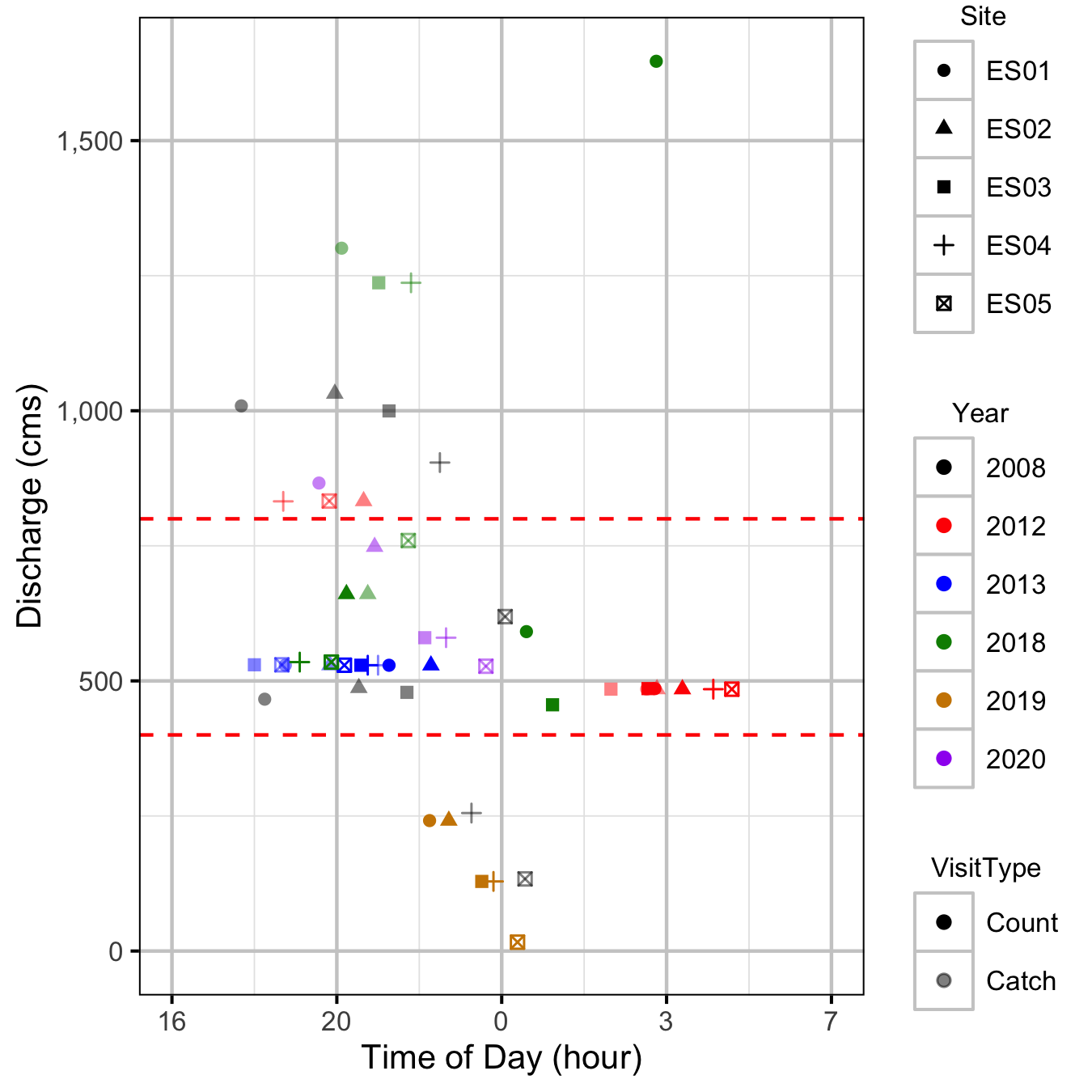
Figure 2. Mean discharge for the period three hours before and during each boat visit. The target discharge range is indicated by the horizontal red dashed lines.

figures/discharge/backpack-visit.png

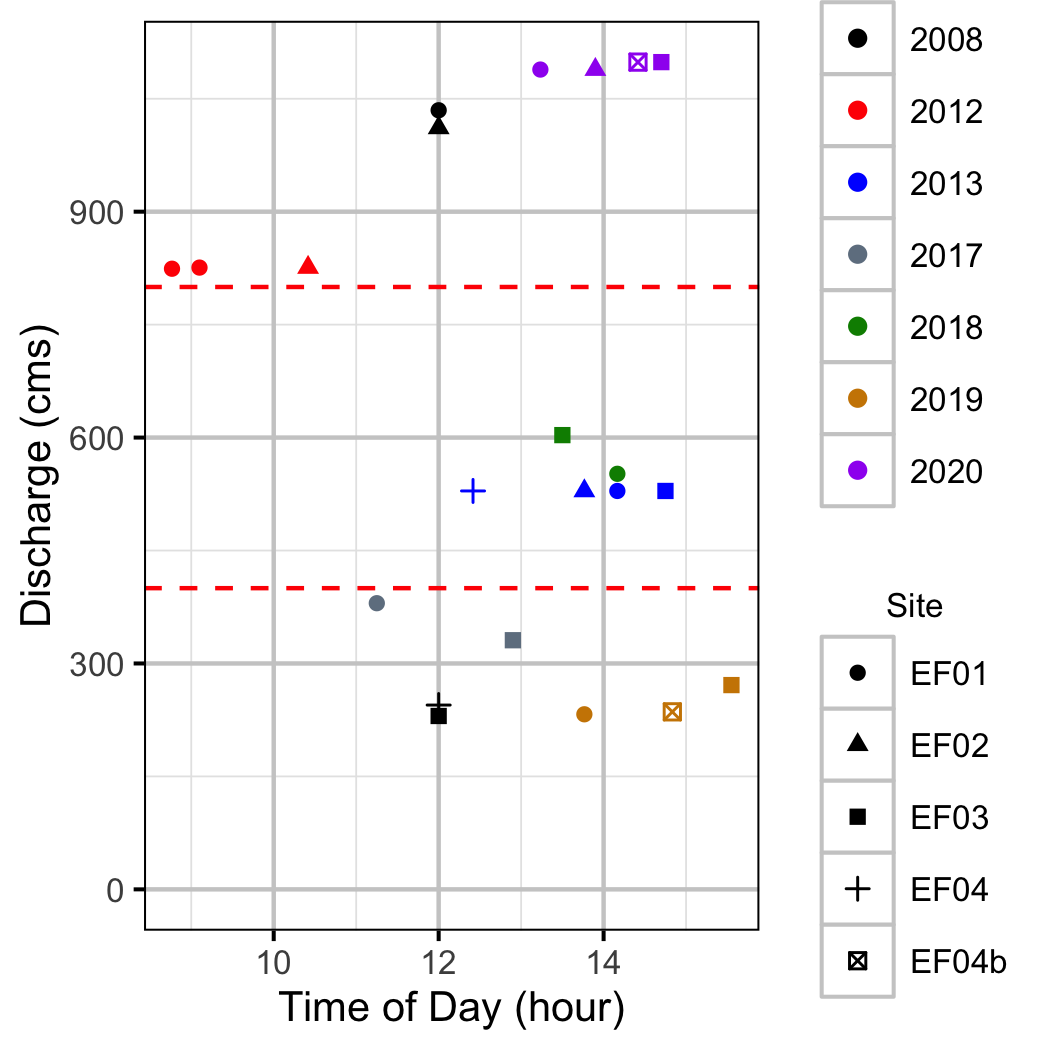
Figure 3. Mean discharge for the period three hours before and during each backpack visit. The target discharge range is indicated by the horizontal red dashed lines.

Condition

figures/condition/year.png

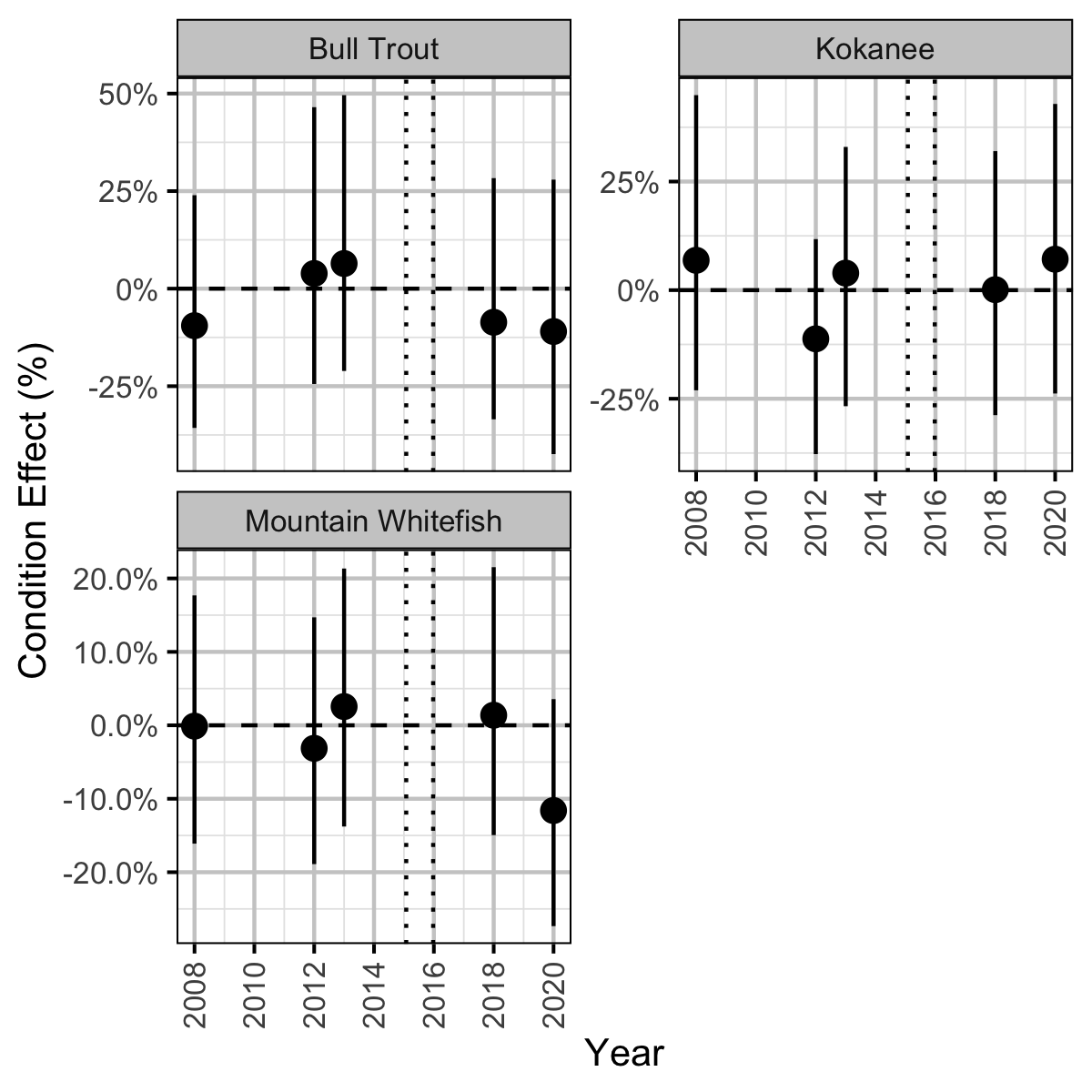
Figure 4. Estimated percent change in body condition by year relative to a typical year pre Mica 5 and 6 (with 95% CIs). The vertical dotted lines indicate the installation of Mica 5 and 6, respectively.

figures/condition/period.png

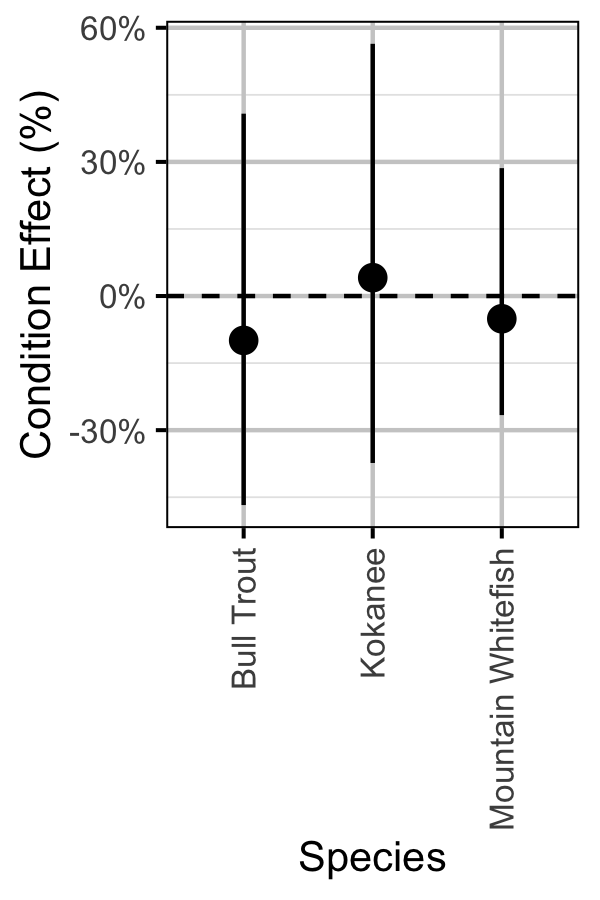
Figure 5. Estimated percent change in body condition associated with Mica 5 and 6 by species (with 95% CIs).

Relative Abundance

figures/count/efficiency.png

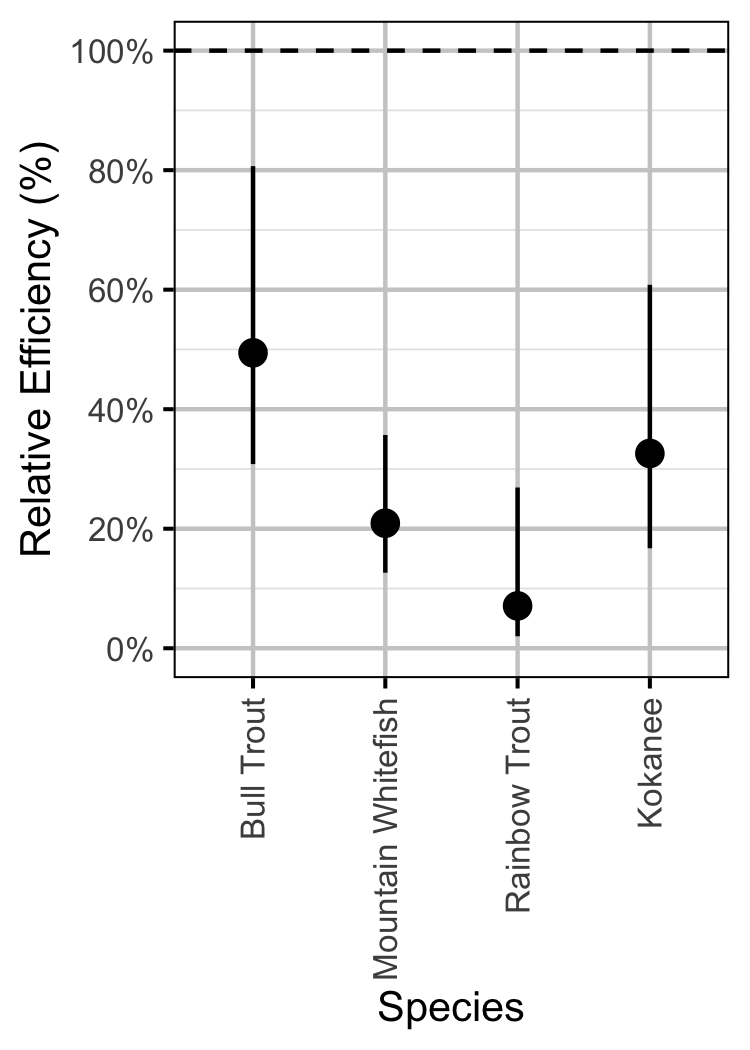
Figure 6. Relative efficiency of catching versus counting (with 95% CRIs).

figures/count/annual_density.png

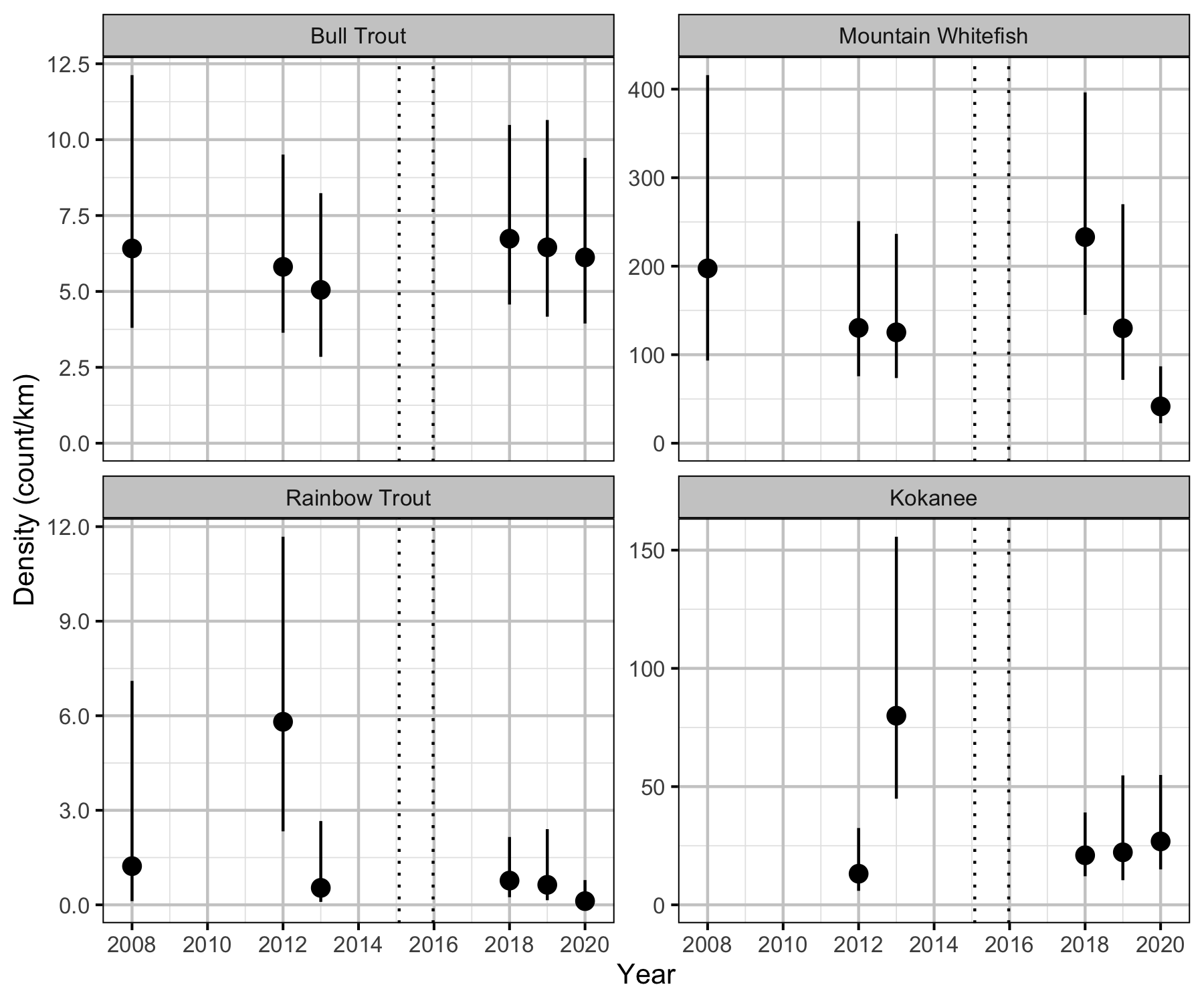
Figure 7. Estimated lineal count density (with 95% CRIs).

figures/count/period.png

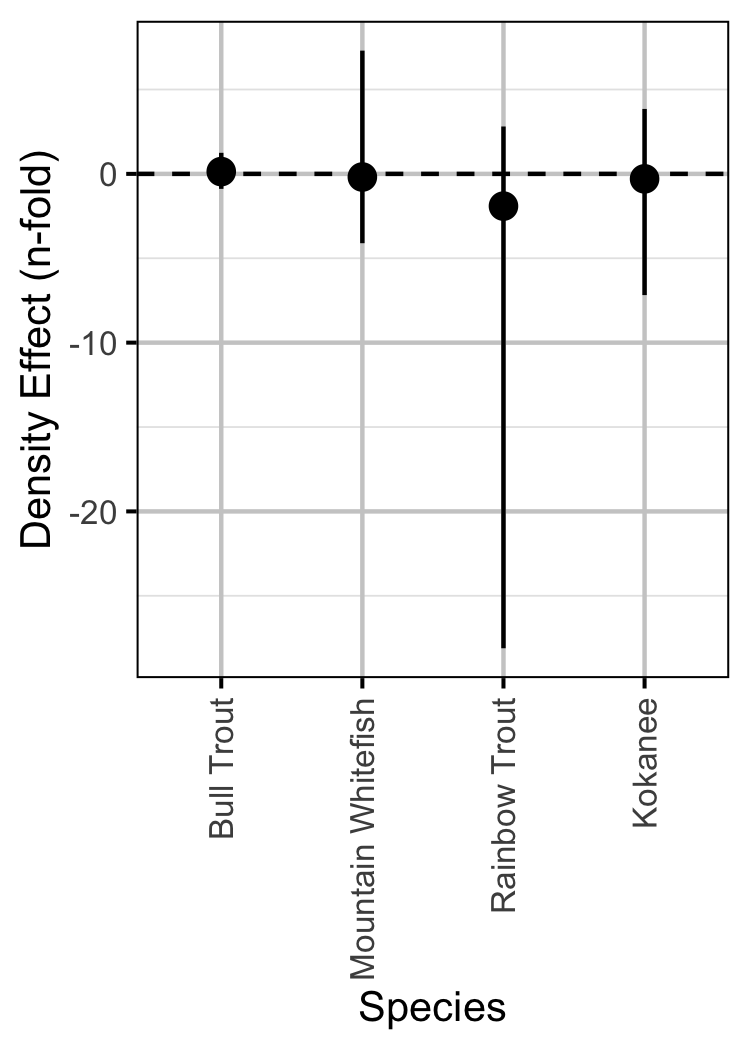
Figure 8. Estimated effect of Mica 5 and 6 on the lineal count density (with 95% CRIs).

figures/count/density.png

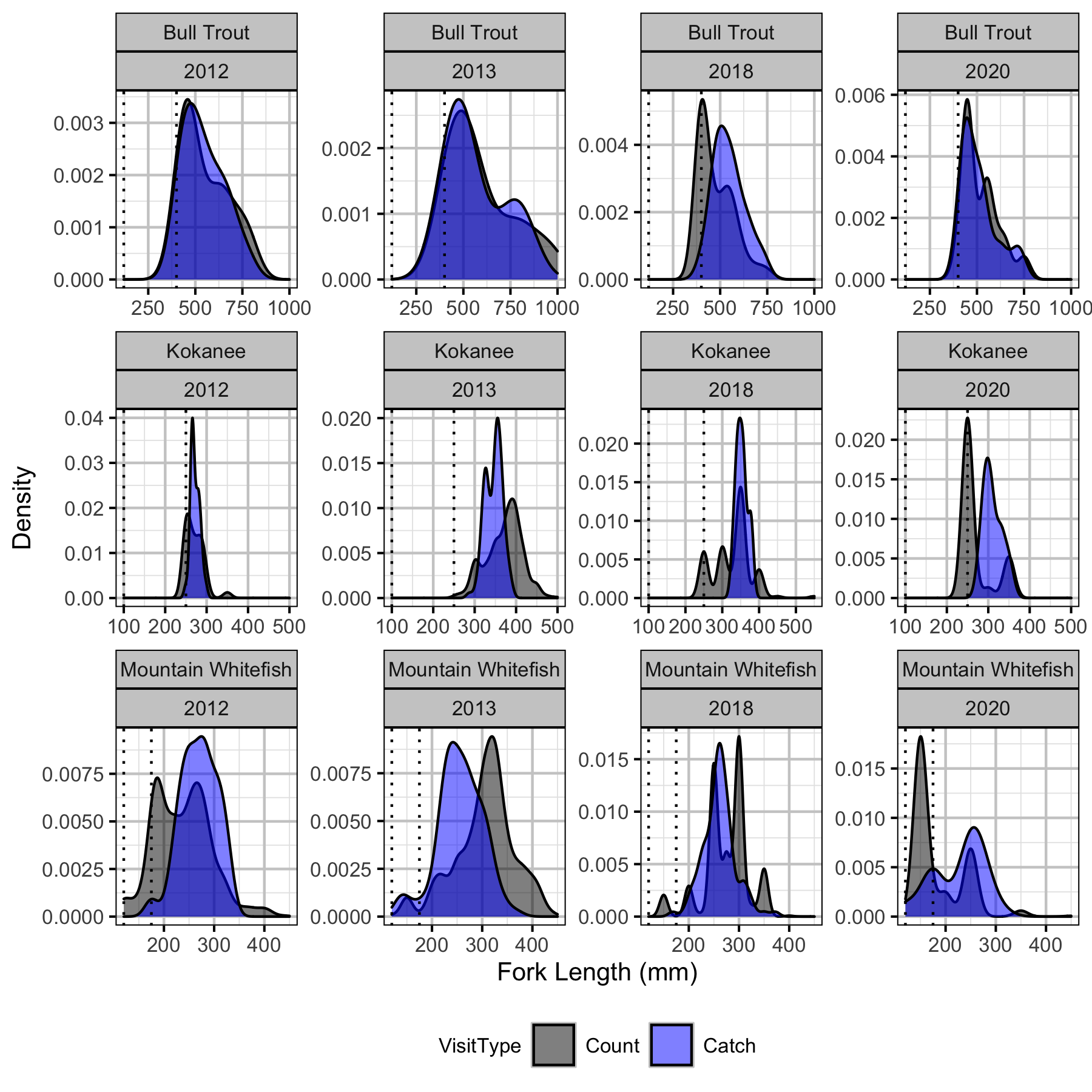
Figure 9. Length density by species and year for boat count versus boat catch for years with fry and juvenile cutoffs indicated by dotted vertical lines.

Bull Trout

figures/count/Bull Trout/Adult/frequency.png

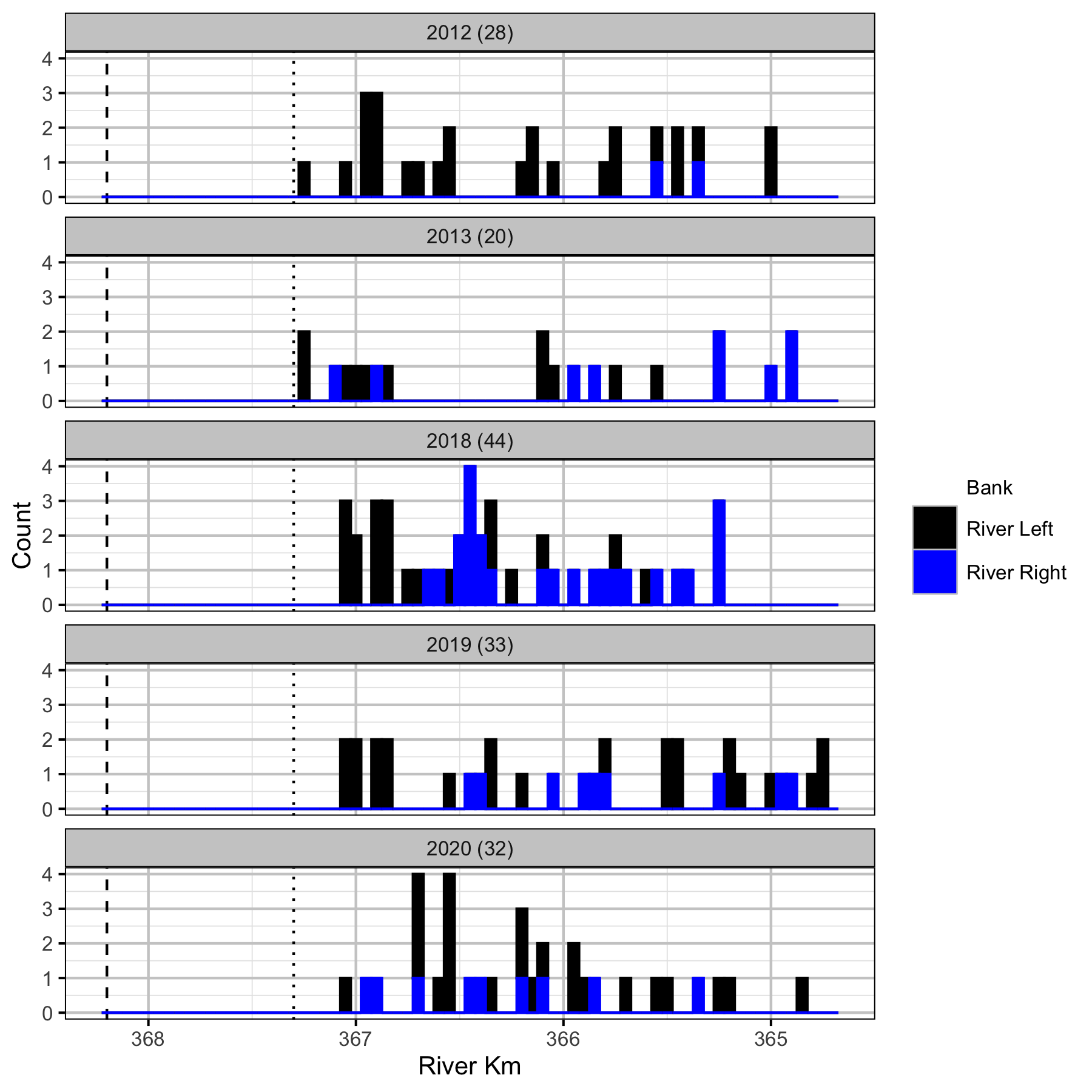
Figure 10. Boat counts by river km and bank for adult Bull Trout. Mica Dam is indicated by the vertical dashed line and the log boom by the vertical dotted line. The total count is in brackets after the year.

Mountain Whitefish

figures/count/Mountain Whitefish/Juvenile/frequency.png

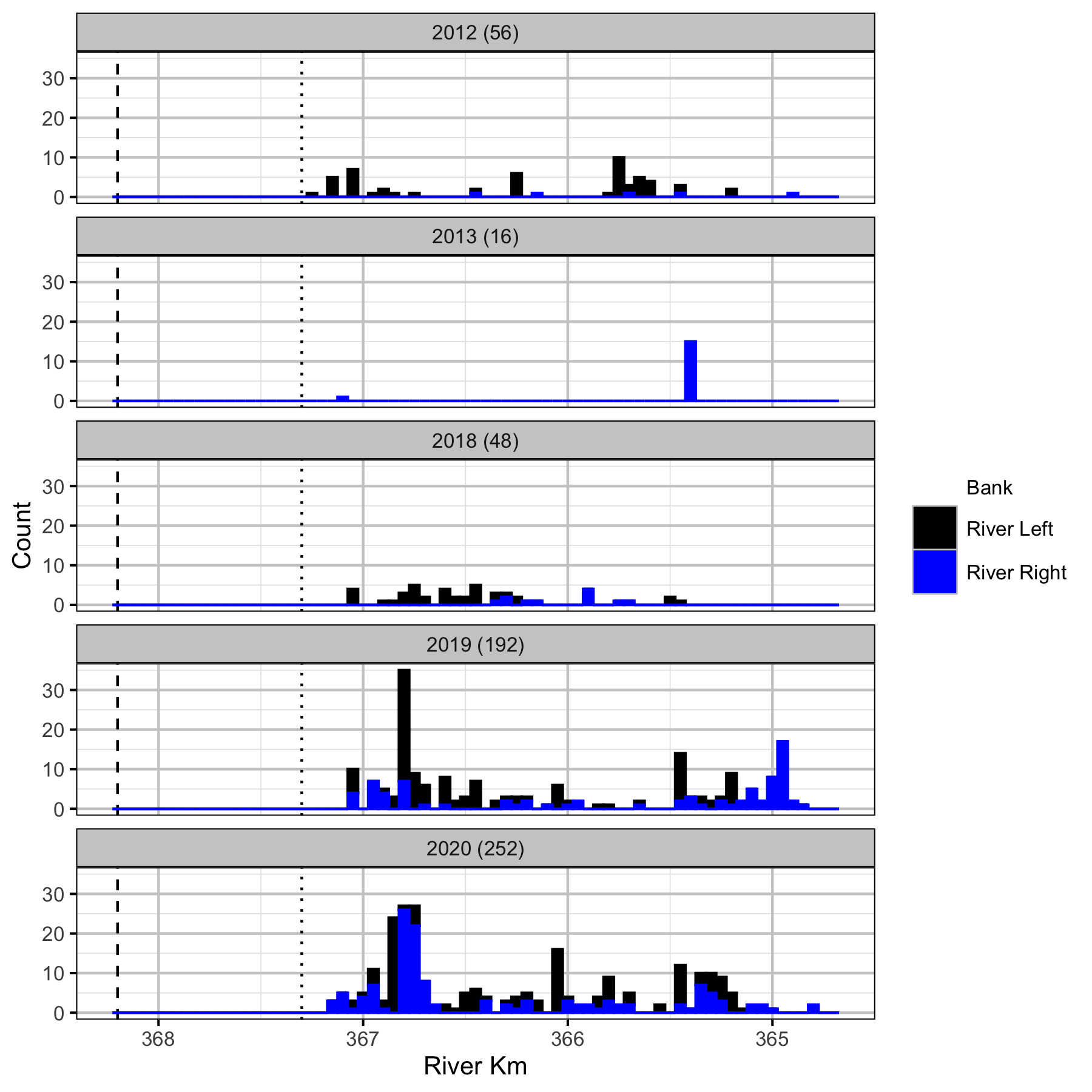
Figure 11. Boat counts by river km and bank for juvenile Mountain Whitefish. Mica Dam is indicated by the vertical dashed line and the log boom by the vertical dotted line. The total count is in brackets after the year.

figures/count/Mountain Whitefish/Adult/frequency.png

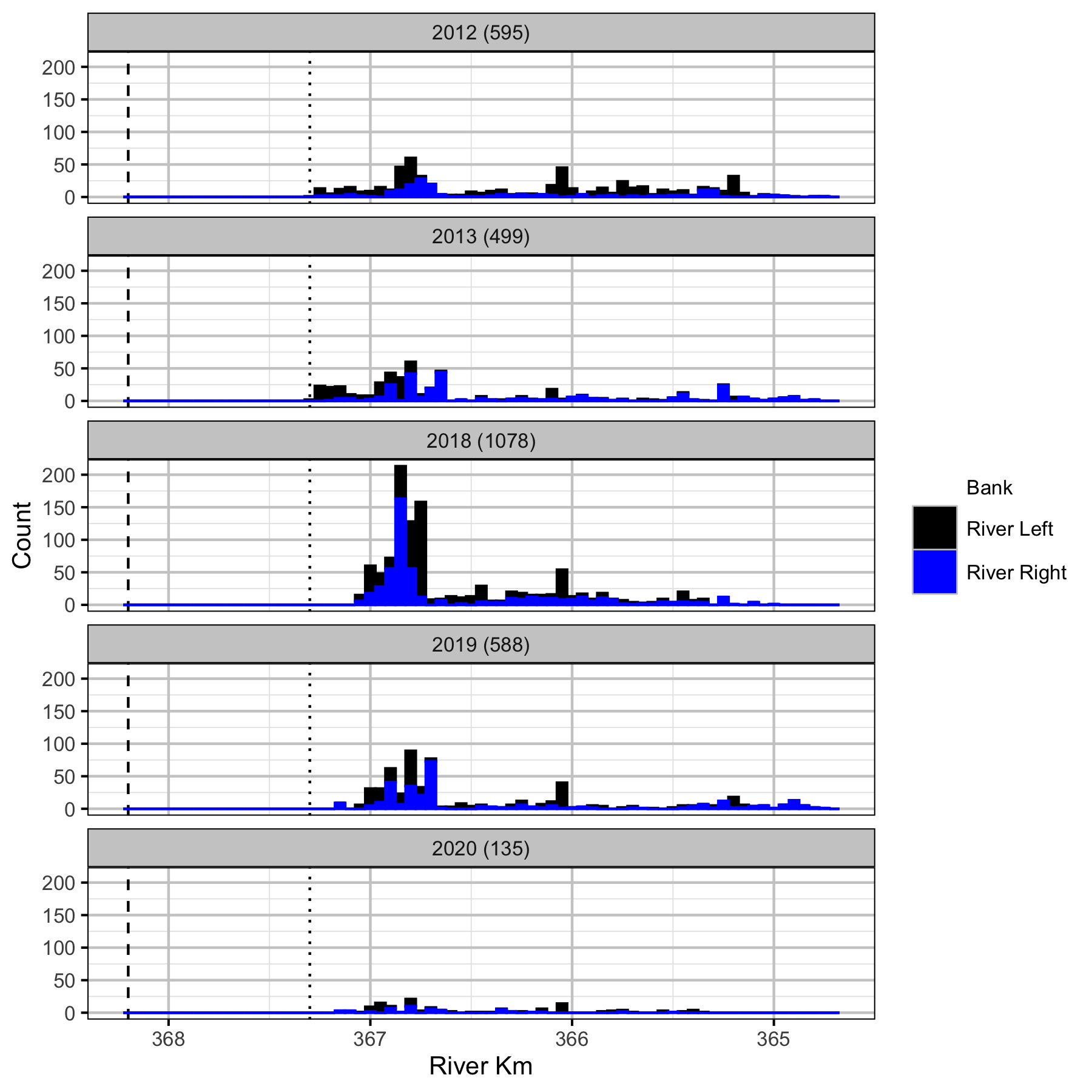
Figure 12. Boat counts by river km and bank for adult Mountain Whitefish. Mica Dam is indicated by the vertical dashed line and the log boom by the vertical dotted line. The total count is in brackets after the year.

Rainbow Trout

figures/count/Rainbow Trout/Adult/frequency.png

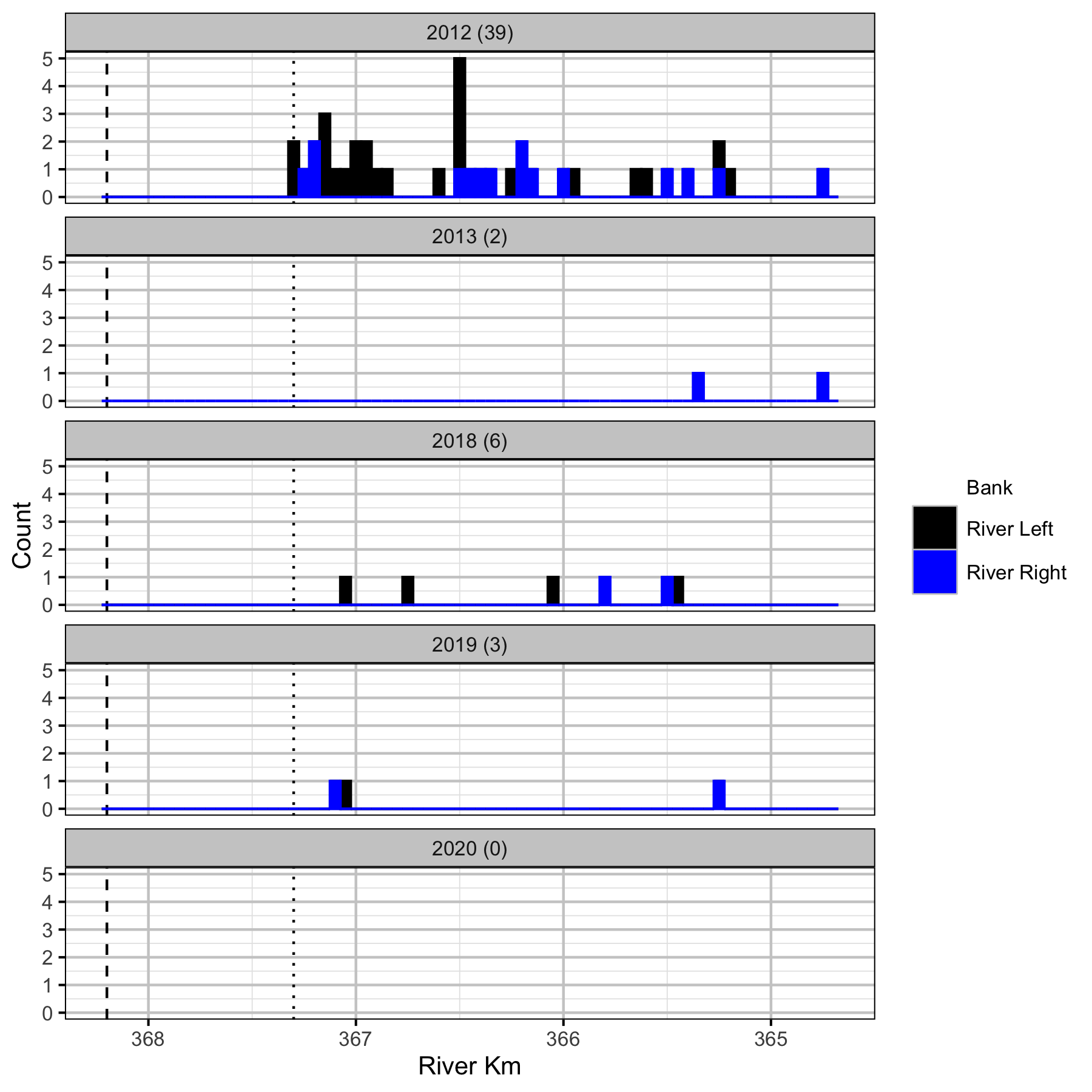
Figure 13. Boat counts by river km and bank for adult Rainbow Trout. Mica Dam is indicated by the vertical dashed line and the log boom by the vertical dotted line. The total count is in brackets after the year.

Kokanee

figures/count/Kokanee/Adult/frequency.png

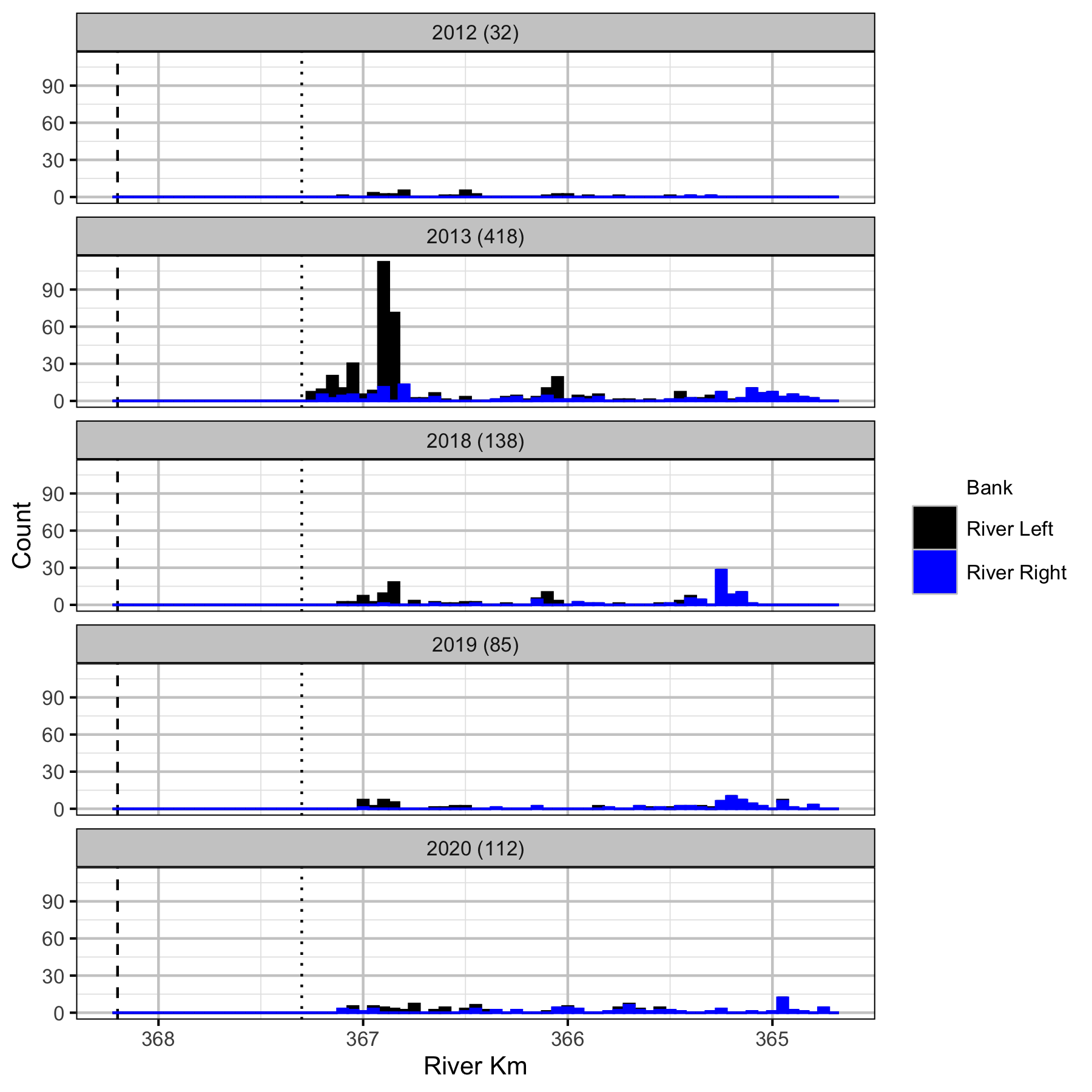
Figure 14. Boat counts by river km and bank for adult Kokanee. Mica Dam is indicated by the vertical dashed line and the log boom by the vertical dotted line. The total count is in brackets after the year.

Backpack Electrofishing

figures/back/visits.png

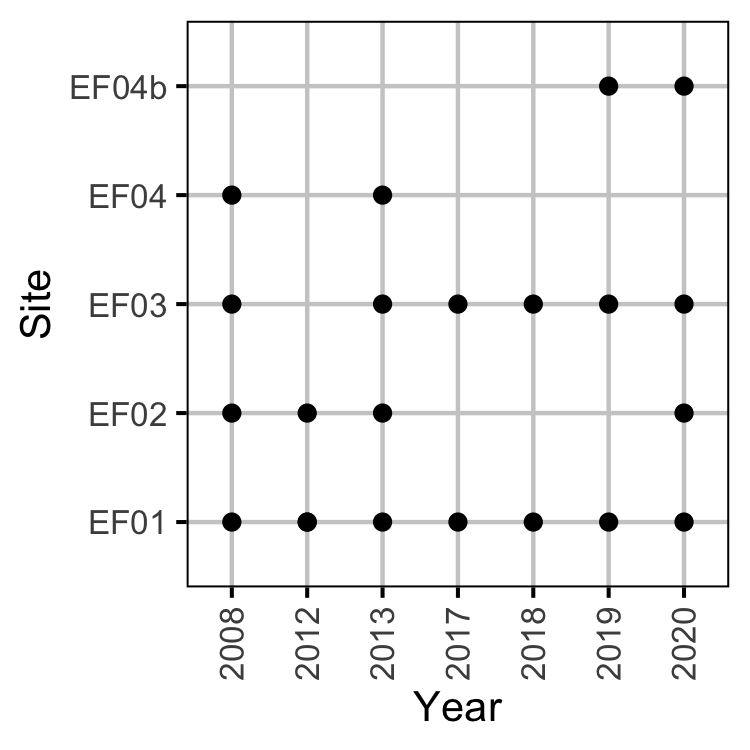
Figure 15. Backpack electrofishing site visits by year.

figures/back/lengthfrequency.png

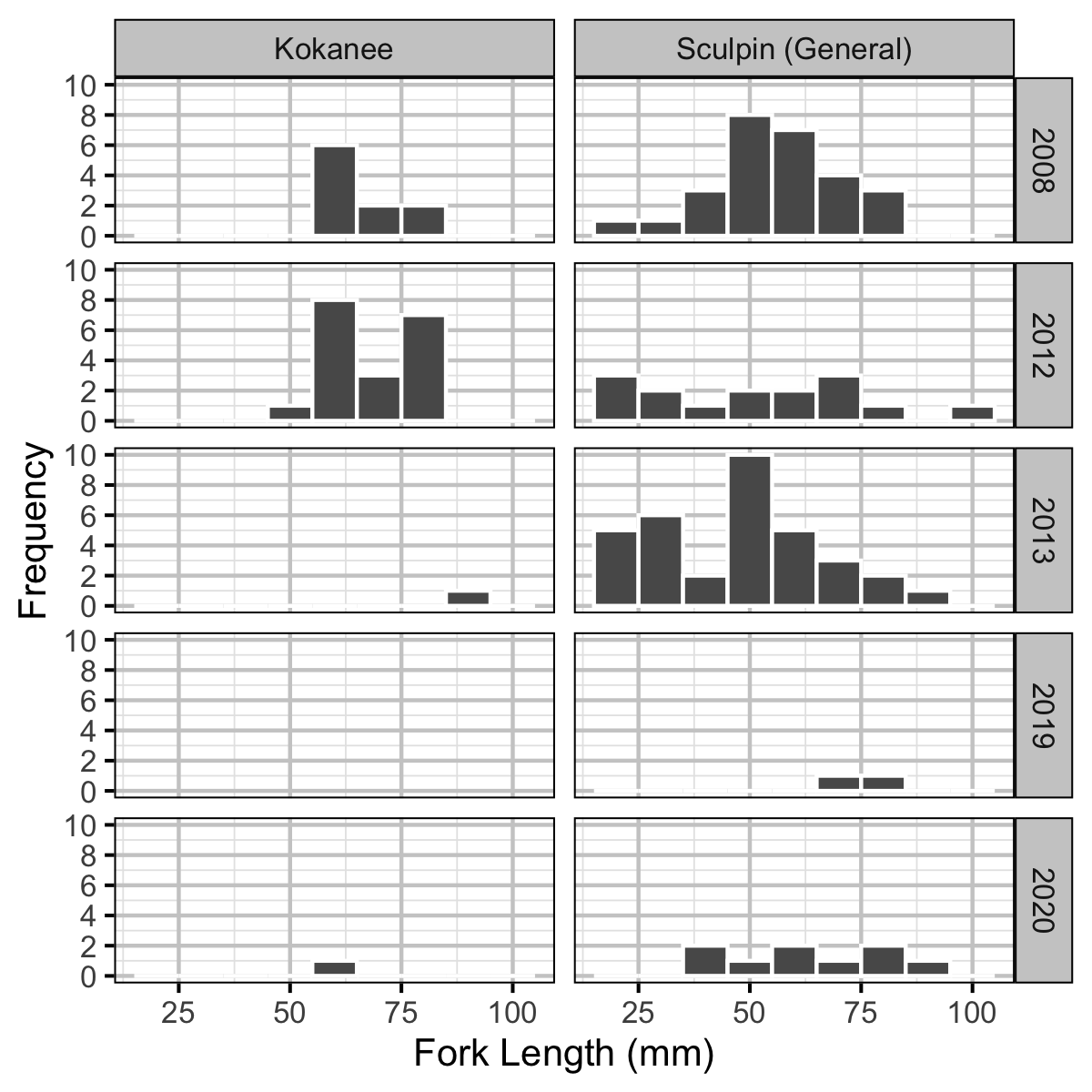
Figure 16. Length-frequency histogram of fish caught by backpack electrofishing by species and year. The plot excludes kokanee greater than 200 mm and one mountain whitefish that was caught in 2019.

Temperature

figures/temperature/bank.png

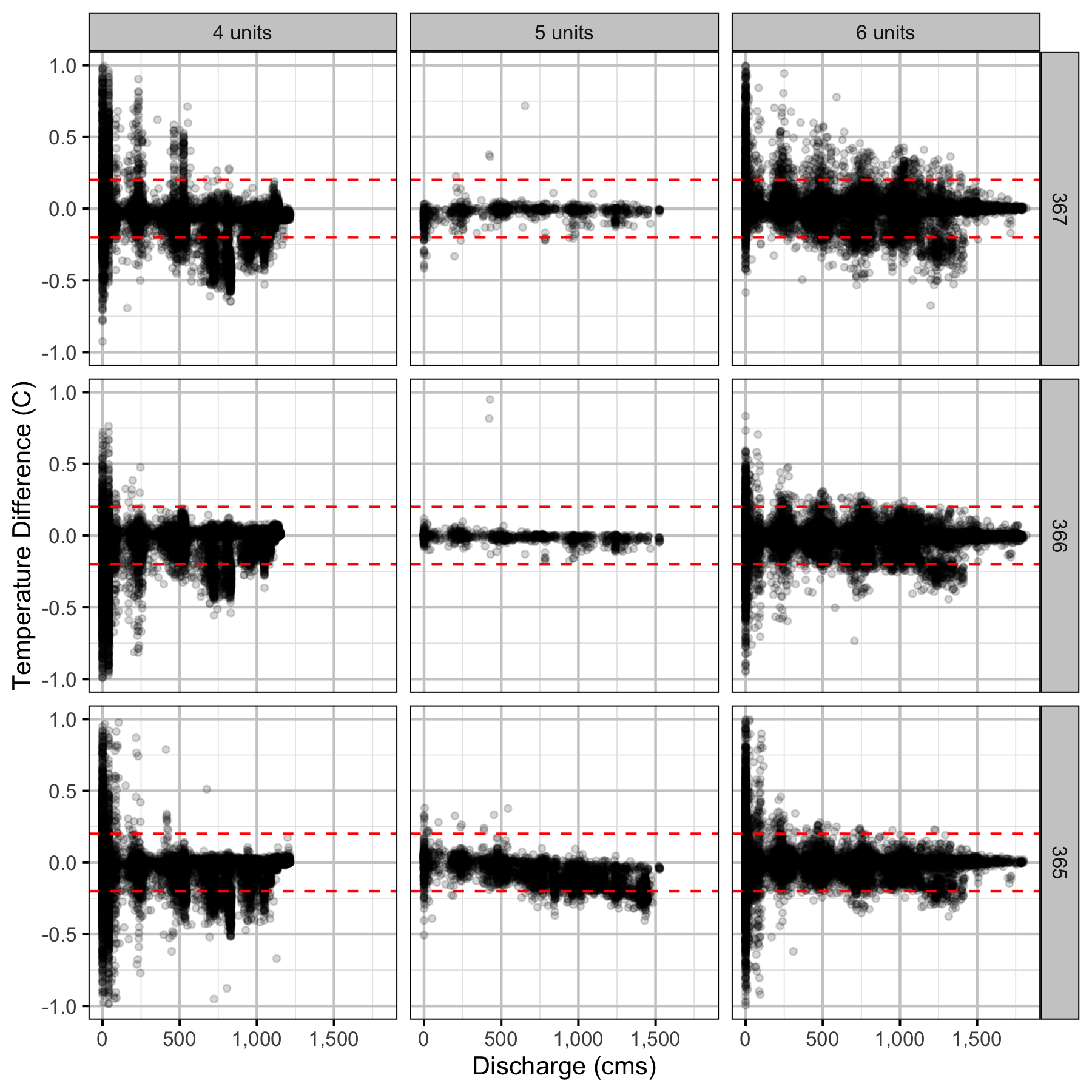
Figure 17. The hourly water temperature difference between the right versus left bank by discharge, regime and river km for absolute differences less than or equal to 1 C. The redd dashed lines indicate the accuracy of a temperature logger.

figures/temperature/bank_all.png

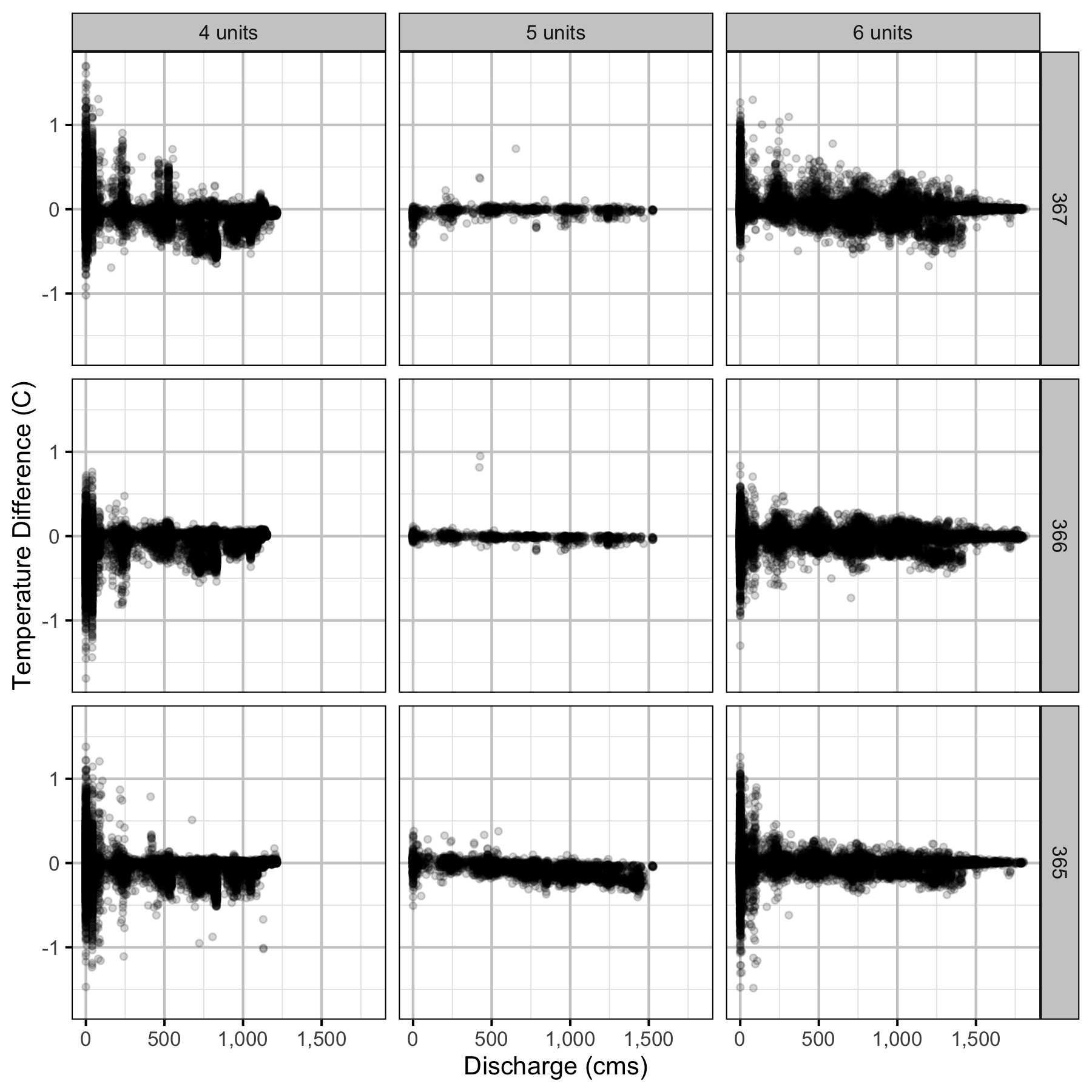
Figure 18. The hourly water temperature difference between the right versus left bank by discharge, regime and river km for all differences.

figures/temperature/distance.png

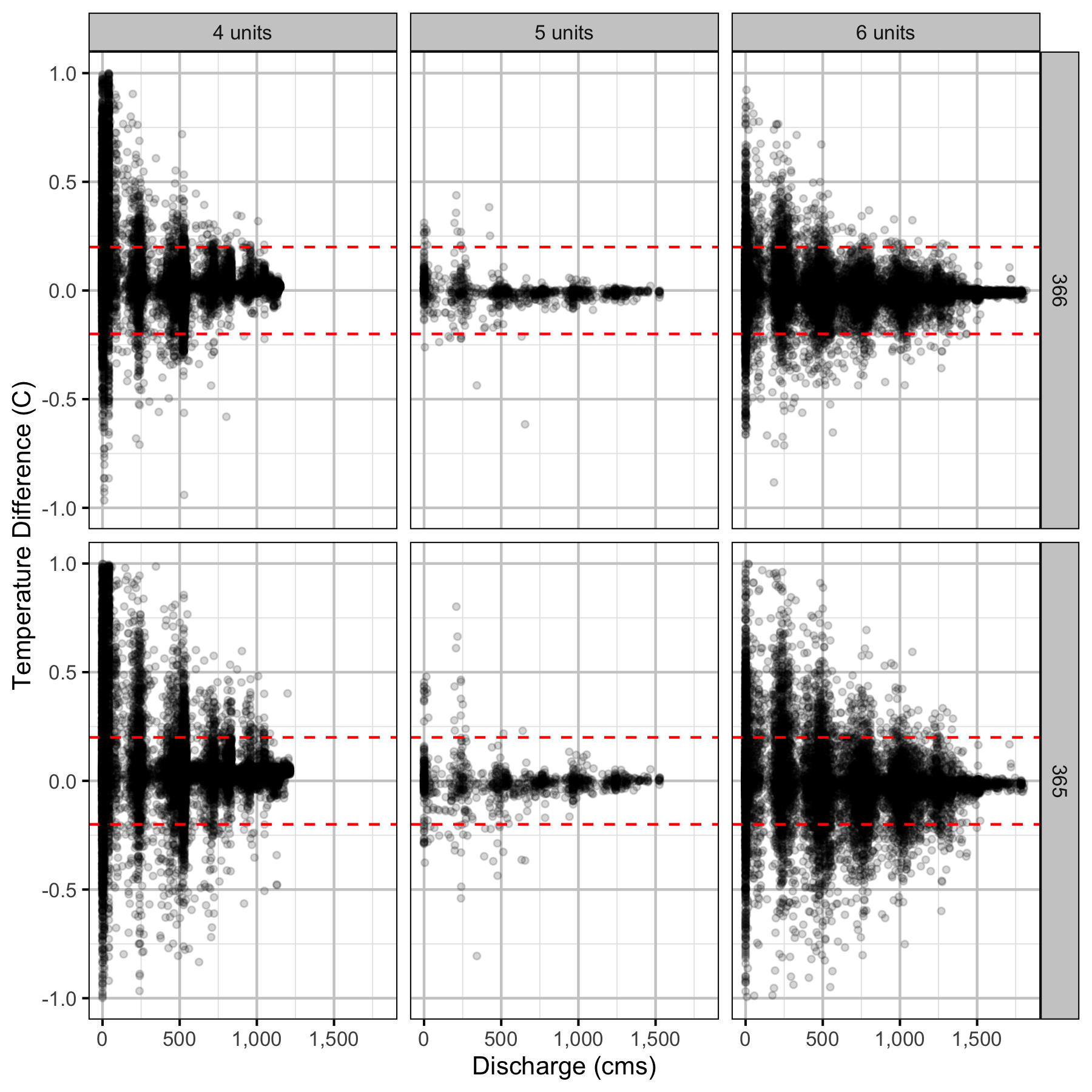
Figure 19. The hourly water temperature difference compared to 367 river km by discharge, regime and river km for absolute differences less than or equal to 1.0 C. The redd dashed lines indicate the accuracy of a temperature logger.

figures/temperature/distance_all.png

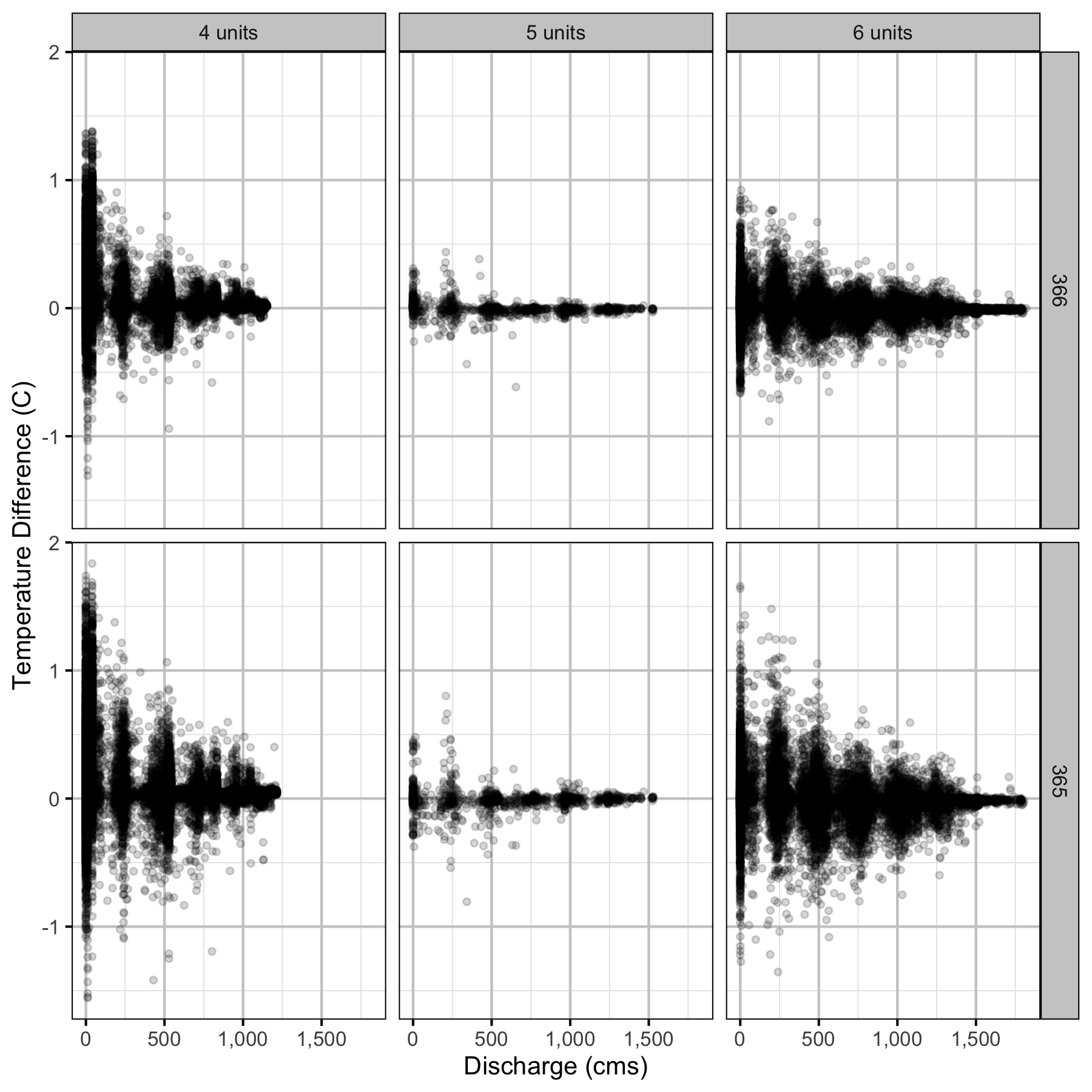
Figure 20. The hourly water temperature difference compared to 367 river km by discharge, regime and river km for all differences.

Tailrace

figures/temperature/tailrace/temperature.png

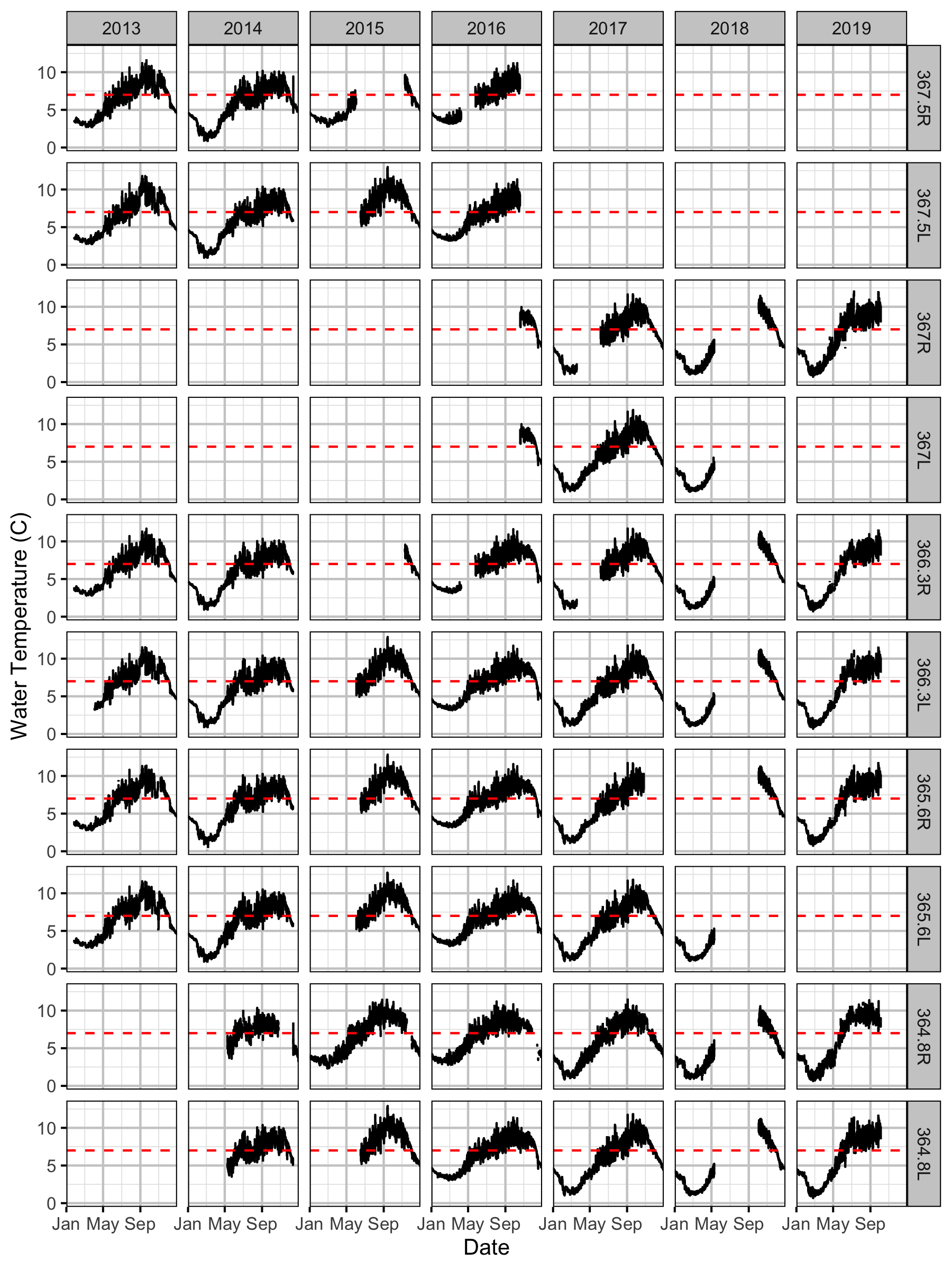
Figure 21. Hourly water temperature in Mica Dam tailrace by date, year and site.

Forebay

figures/temperature/forebay/temperature.png

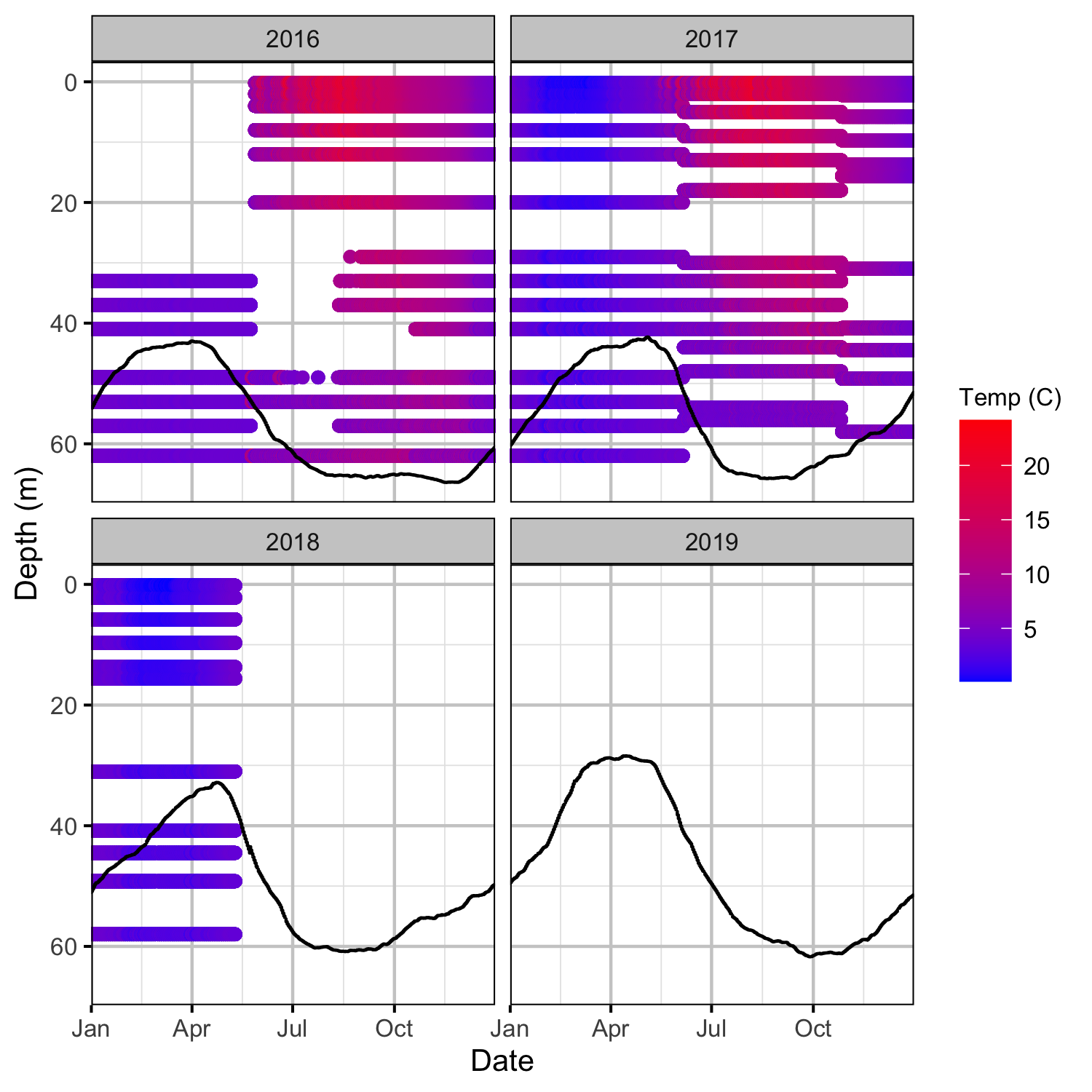
Figure 22. Hourly water temperature in Mica Dam forebay by date, depth and year.

Forebay and Tailrace

figures/mca/thermistors.png

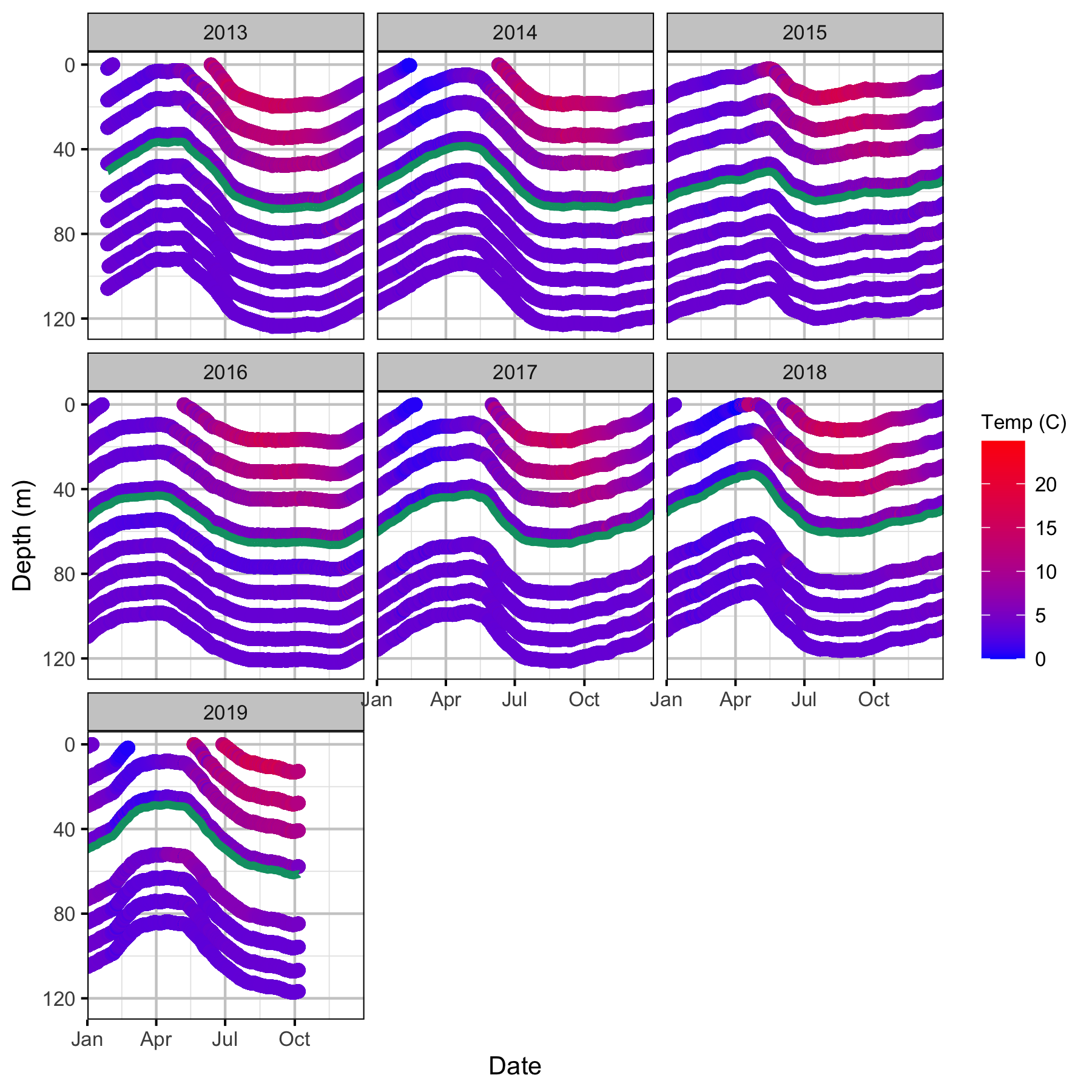
Figure 23. The dam thermistor water temperatures by date, depth and year. The green line indicates the turbine intake depth of 686.41 masl.

figures/mca/actual.png

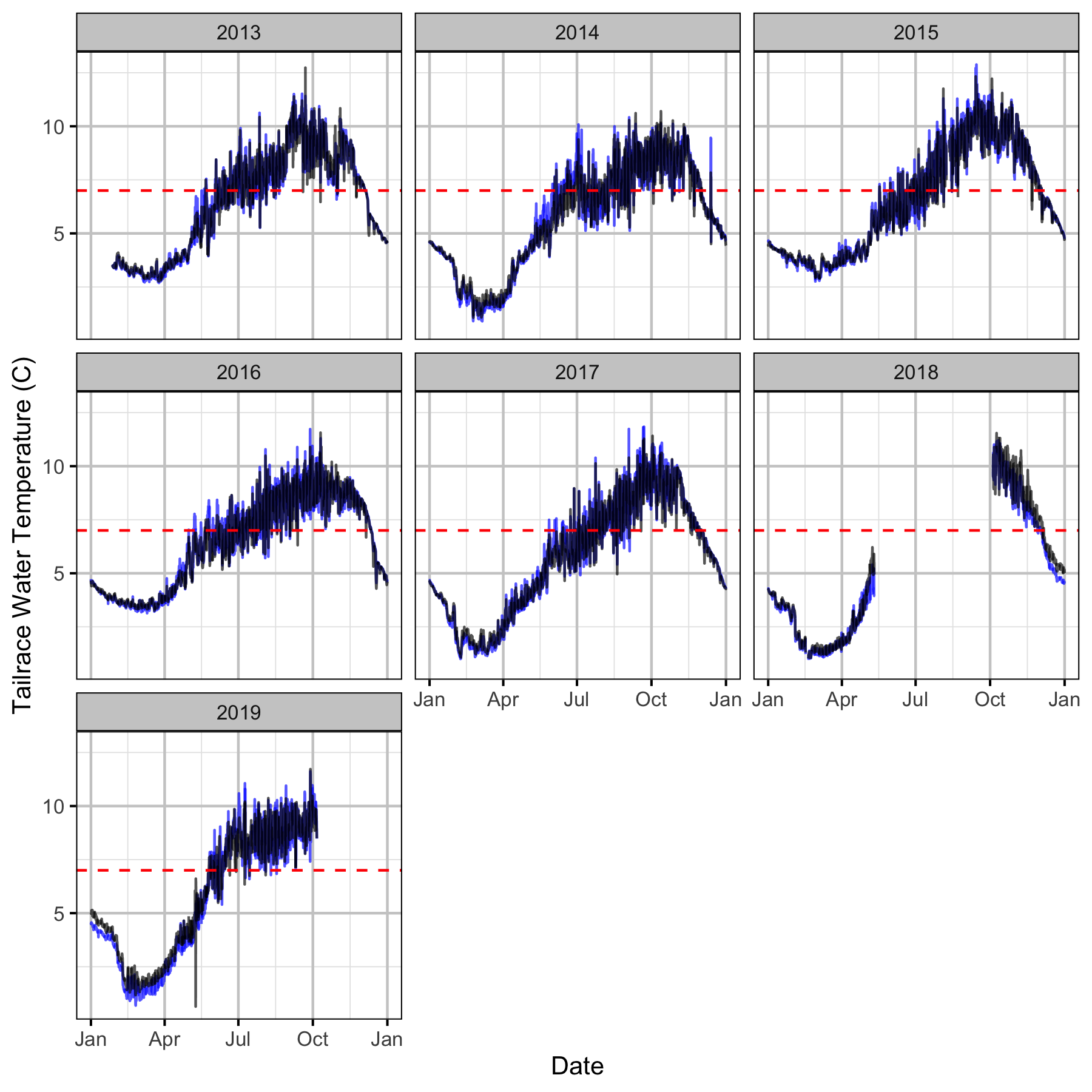
Figure 24. The actual (in red) and estimated (in black) hourly tailrace water temperature by date and year.

figures/mca/raw.png

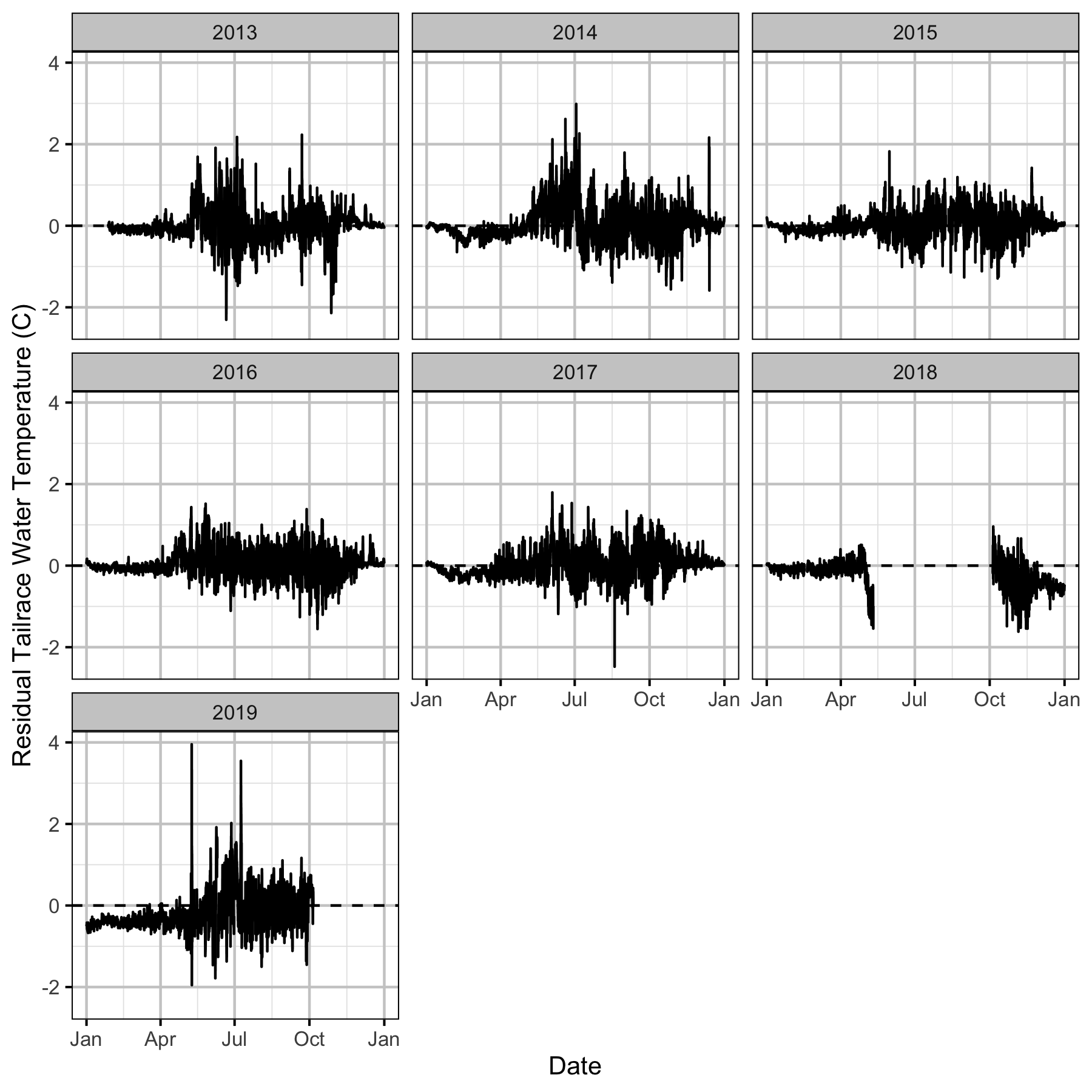
Figure 25. The raw residual hourly tailrace water temperature by date and year.

figures/mca/stratification.png

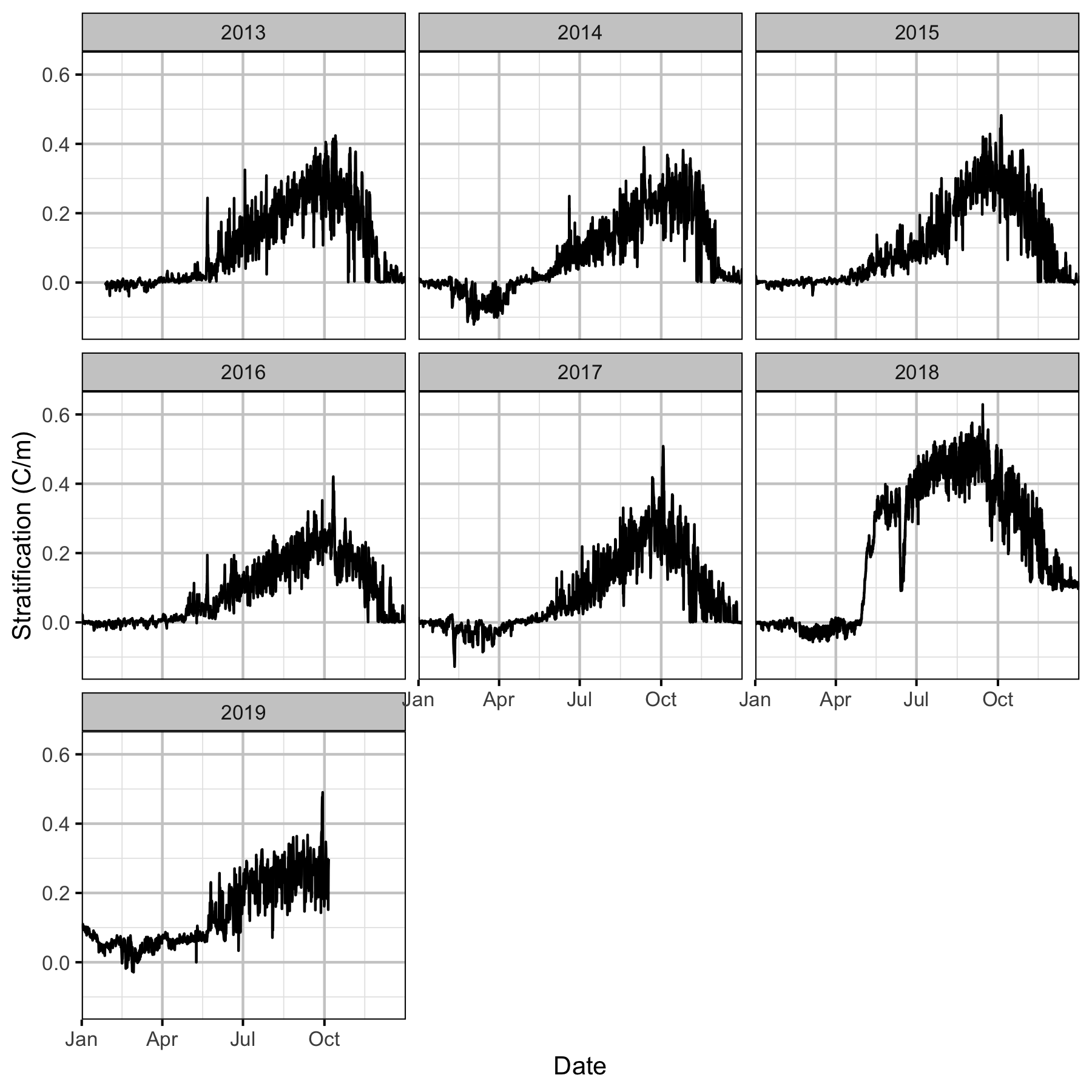
Figure 26. The hourly water temperature stratification between the thermistor at 707 masl and the thermistor at 690 masl by date and year.

figures/mca/turbine.png

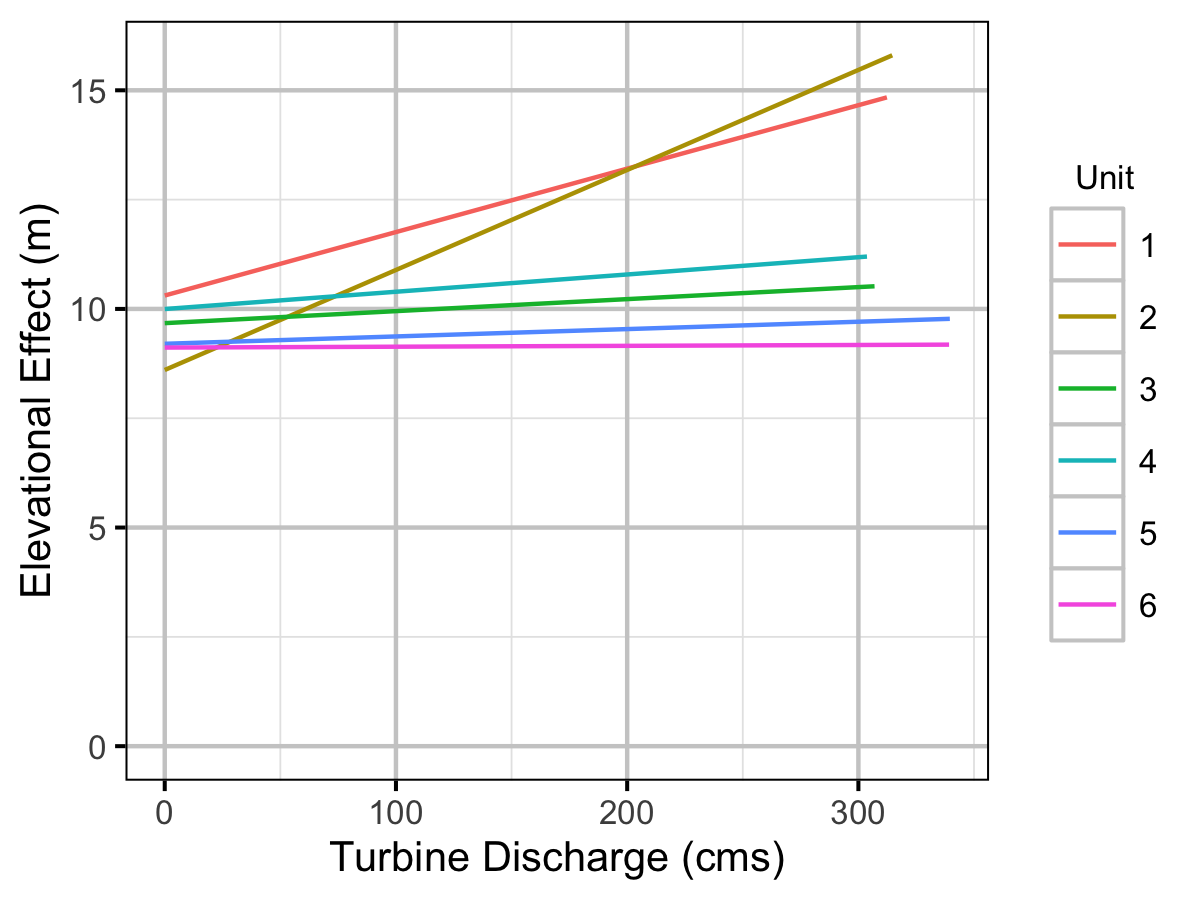
Figure 27. The estimated elevational effect relative to the thermistor at 690 masl by the turbine discharge and unit.

figures/mca/temp.png

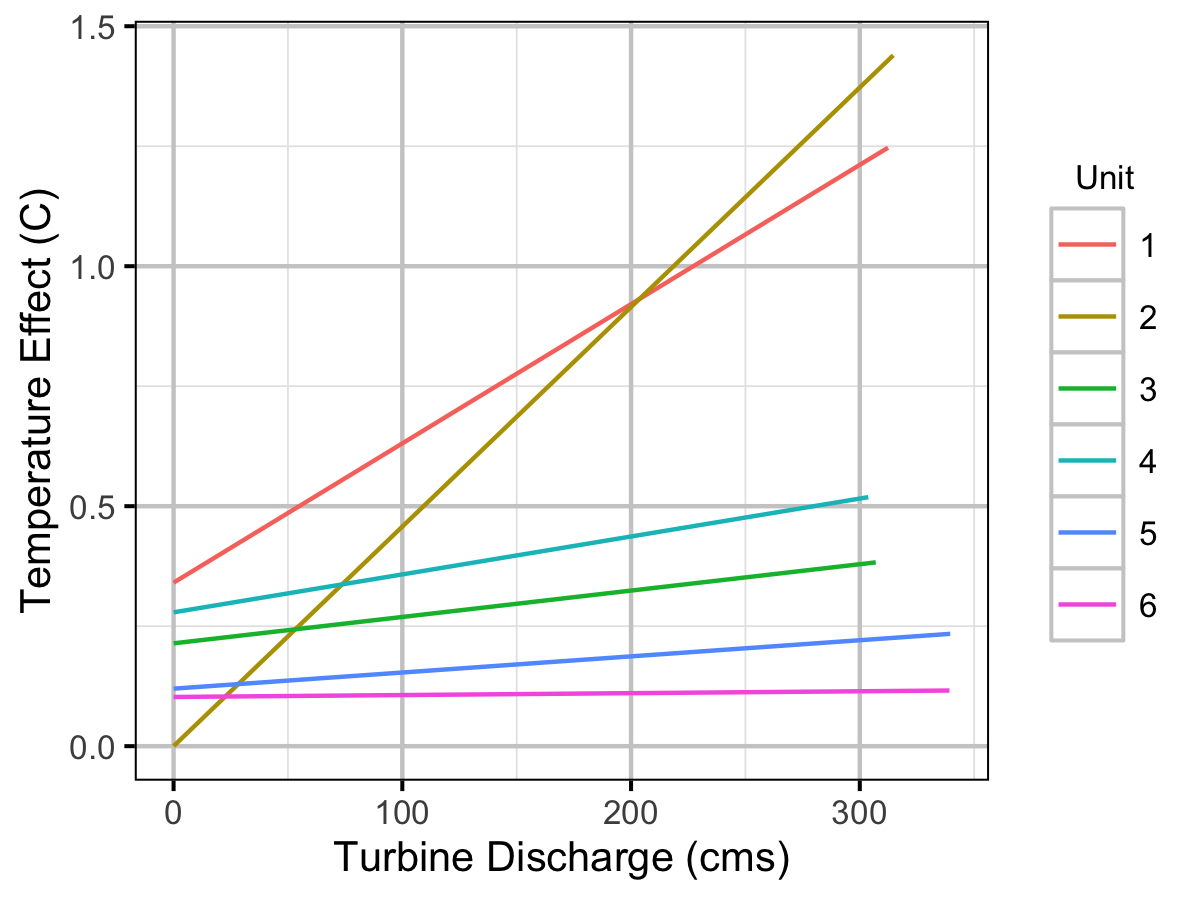
Figure 28. The estimated temperature effect relative to no discharge by the turbine discharge and unit.

figures/mca/air_temp.png

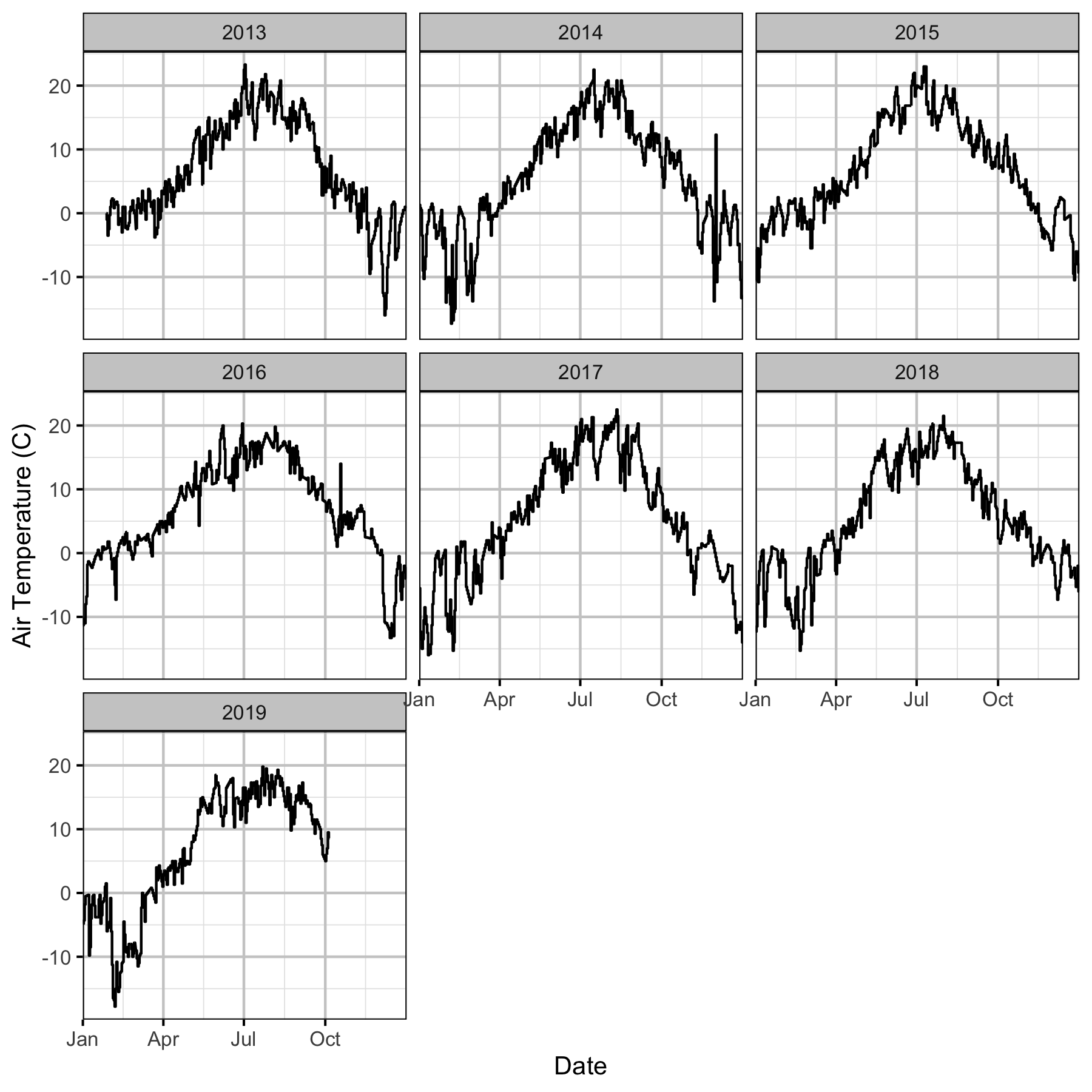
Figure 29. The mean daily air temperature at the Mica weather station by date and year.

figures/mca/air.png

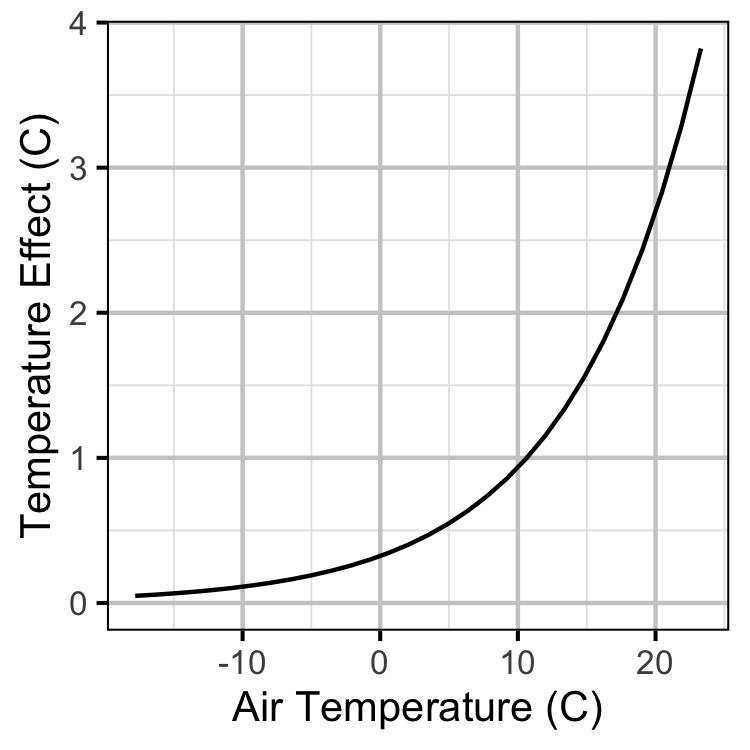
Figure 30. The estimated effect of the difference between the mean daily air temperature and the temperature at the thermistor at 690 masl on the discharge temperature.

Maps

Sites

figures/map/sites/boat-sites.png

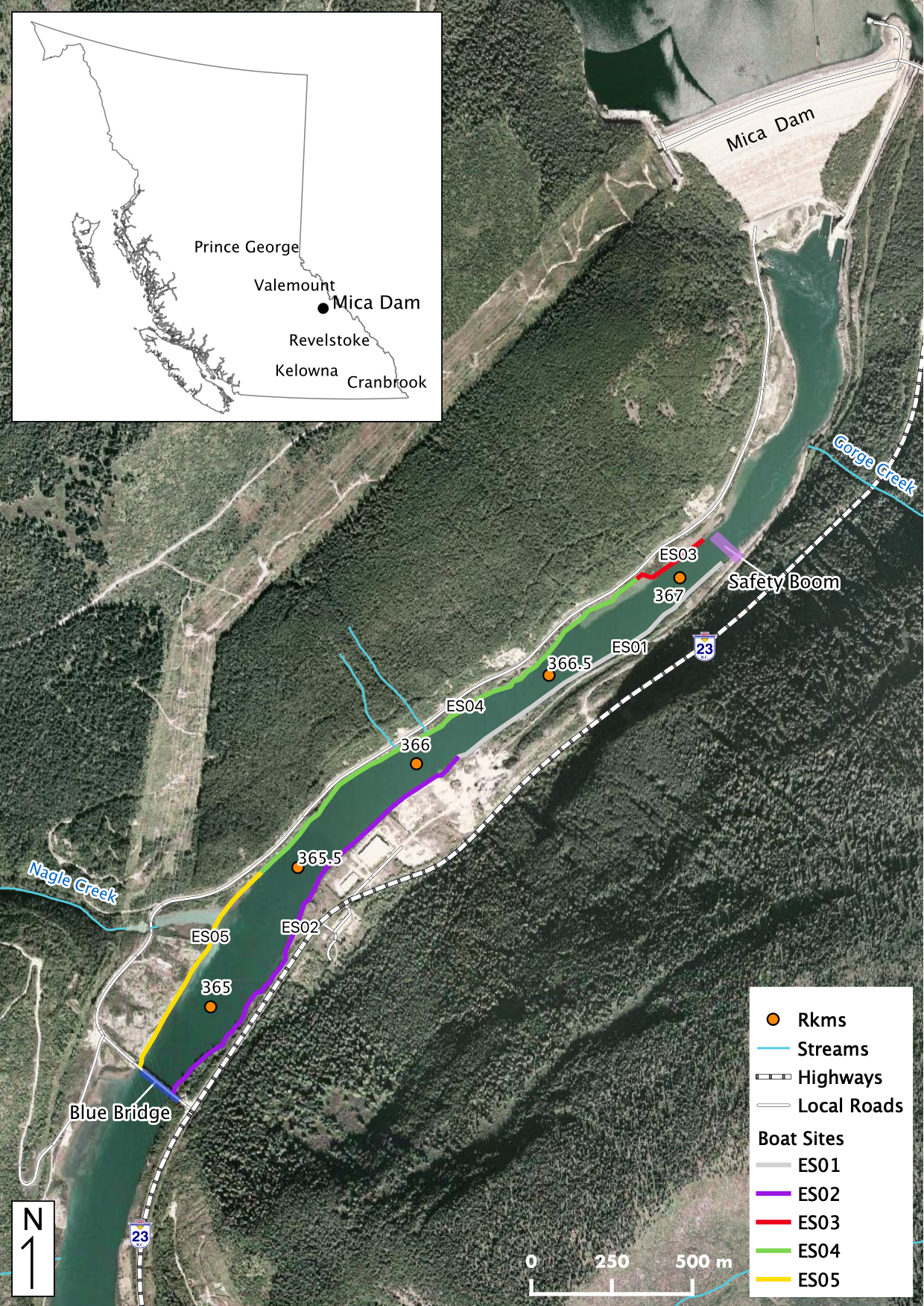
Figure 31. Overview map of Boat Electrofishing (ES) sites.

figures/map/sites/ef-sites.png

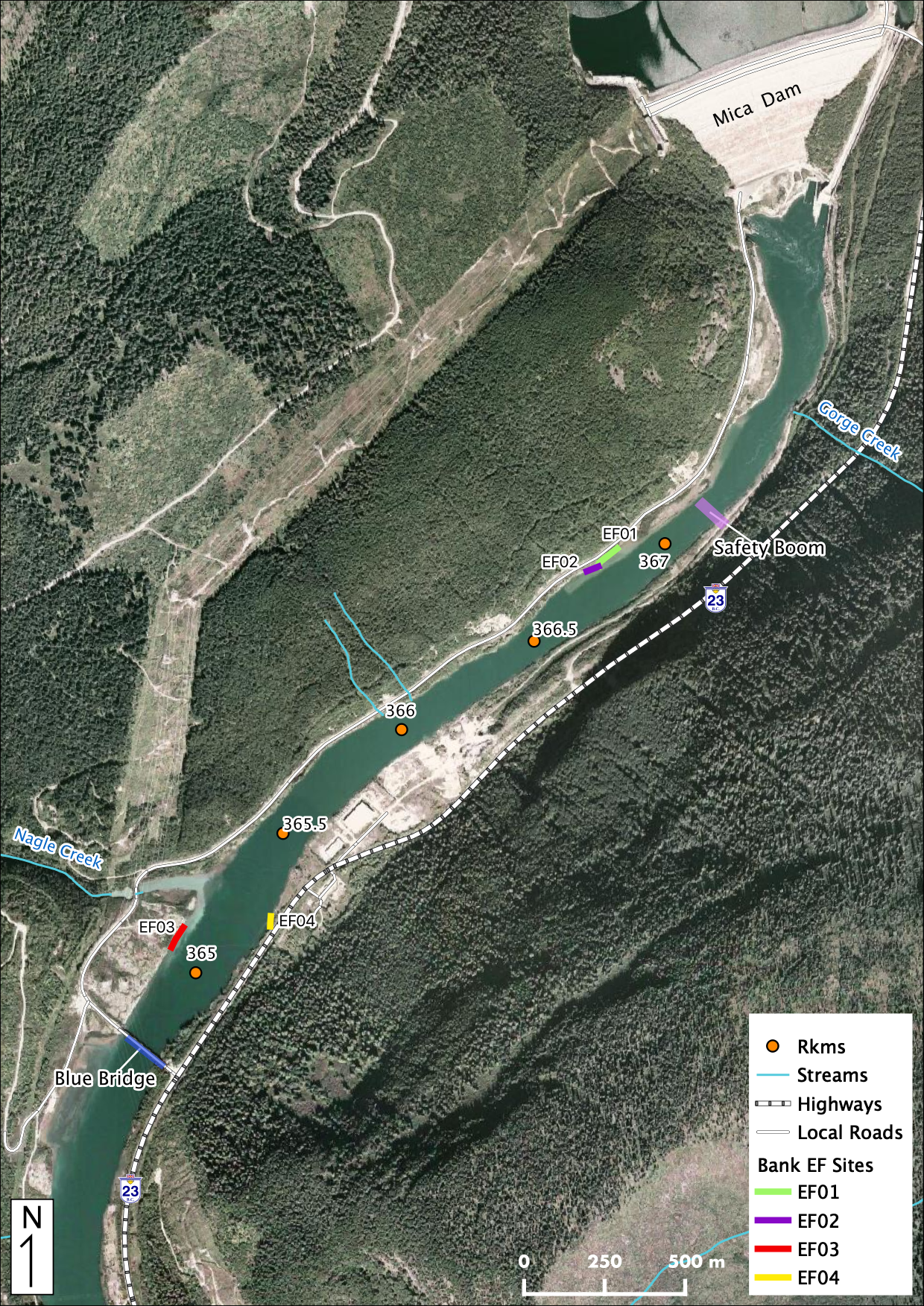
Figure 32. Overview map of Backpack Electrofishing (EF) sites.

figures/map/sites/temperature-loggers.png

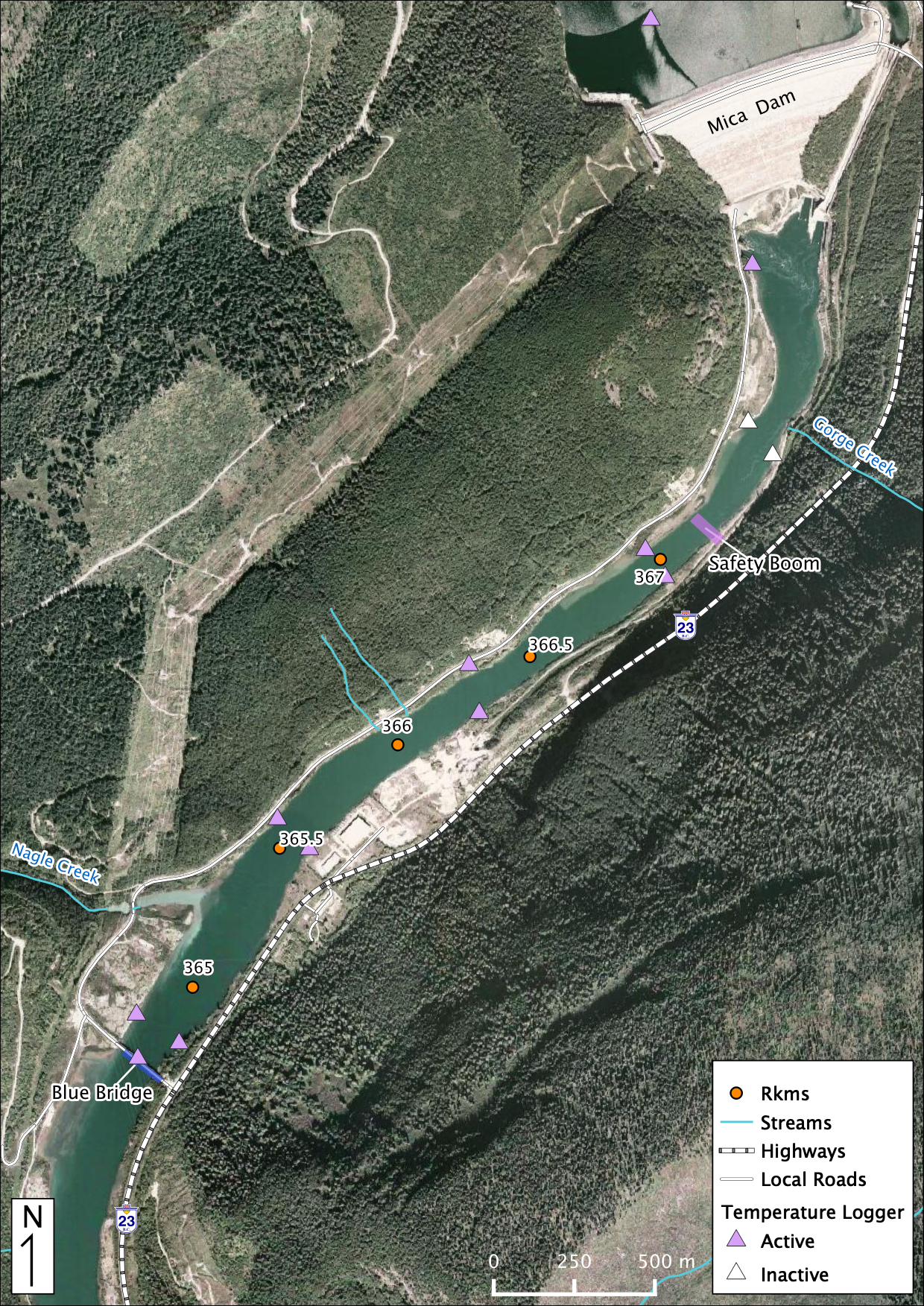
Figure 33. Overview map of Tidbit temperature logger deployment locations for 2019.

Relative Distributions

figures/map/relative-distribution/bt-adult.png

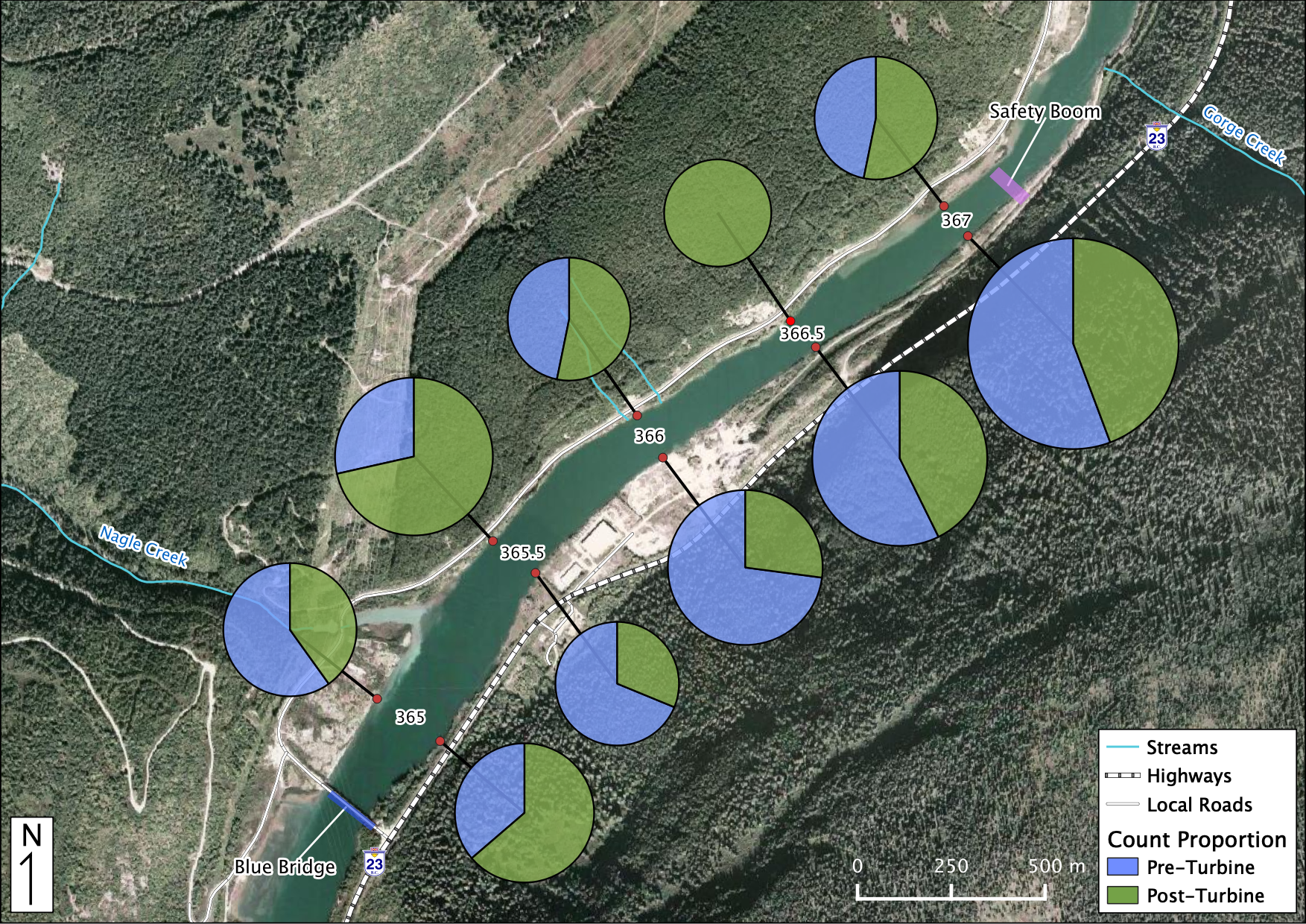
Figure 34. Relative Distribution of Adult Bull Trout. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/bt-juv.png

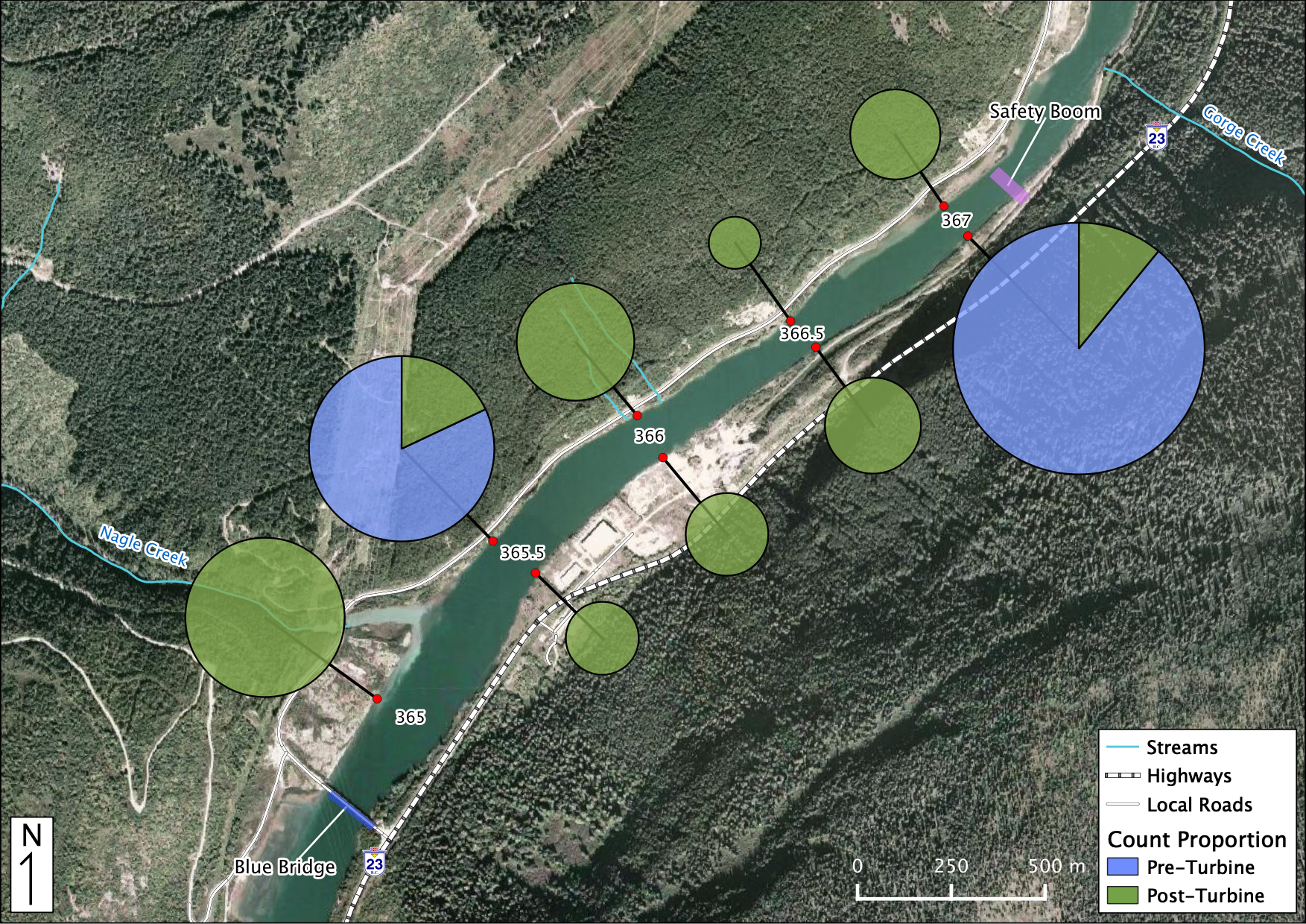
Figure 35. Relative Distribution of Juvenile Bull Trout. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/ko-adult.png

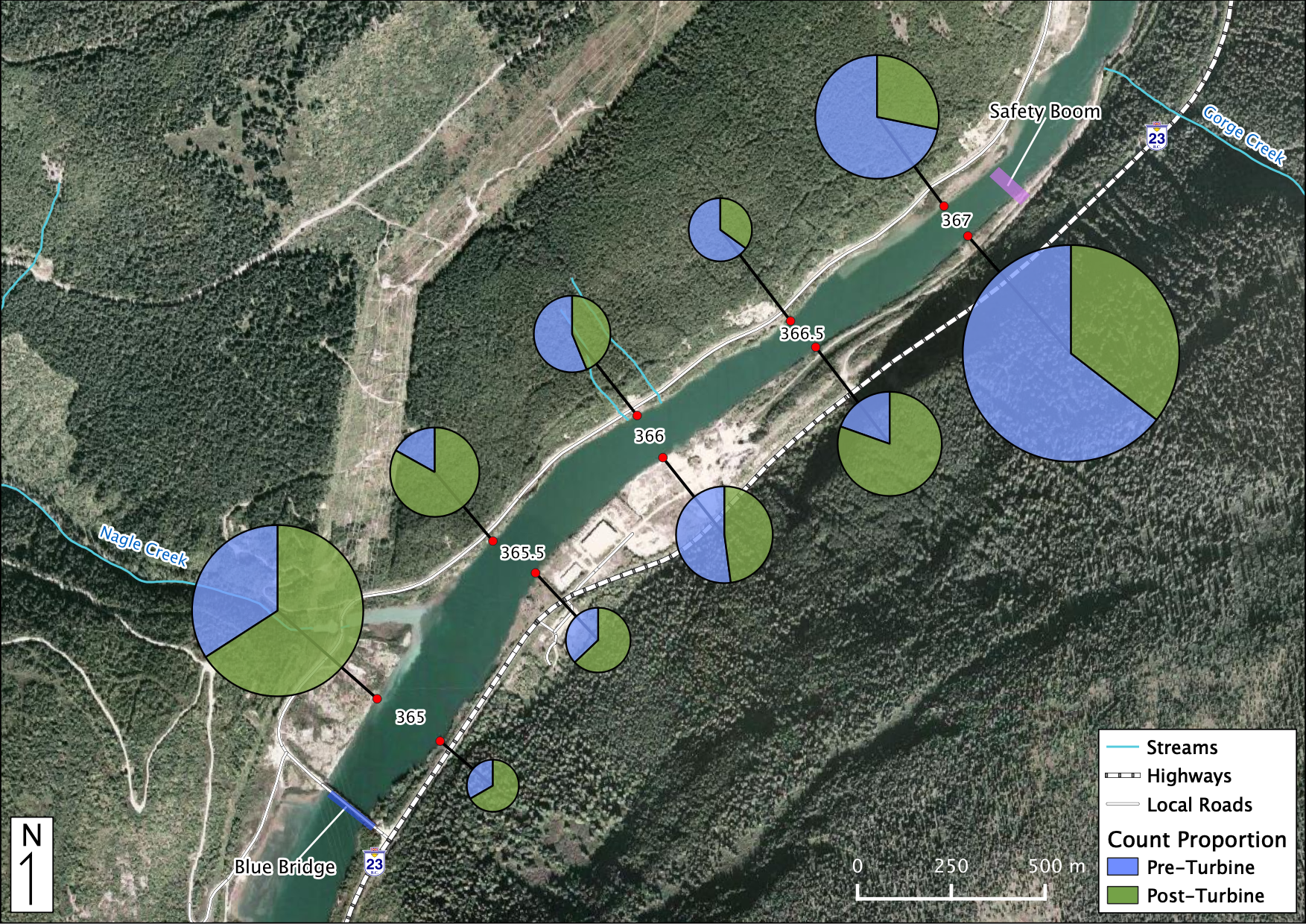
Figure 36. Relative Distribution of Adult Kokanee. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/ko-fry.png

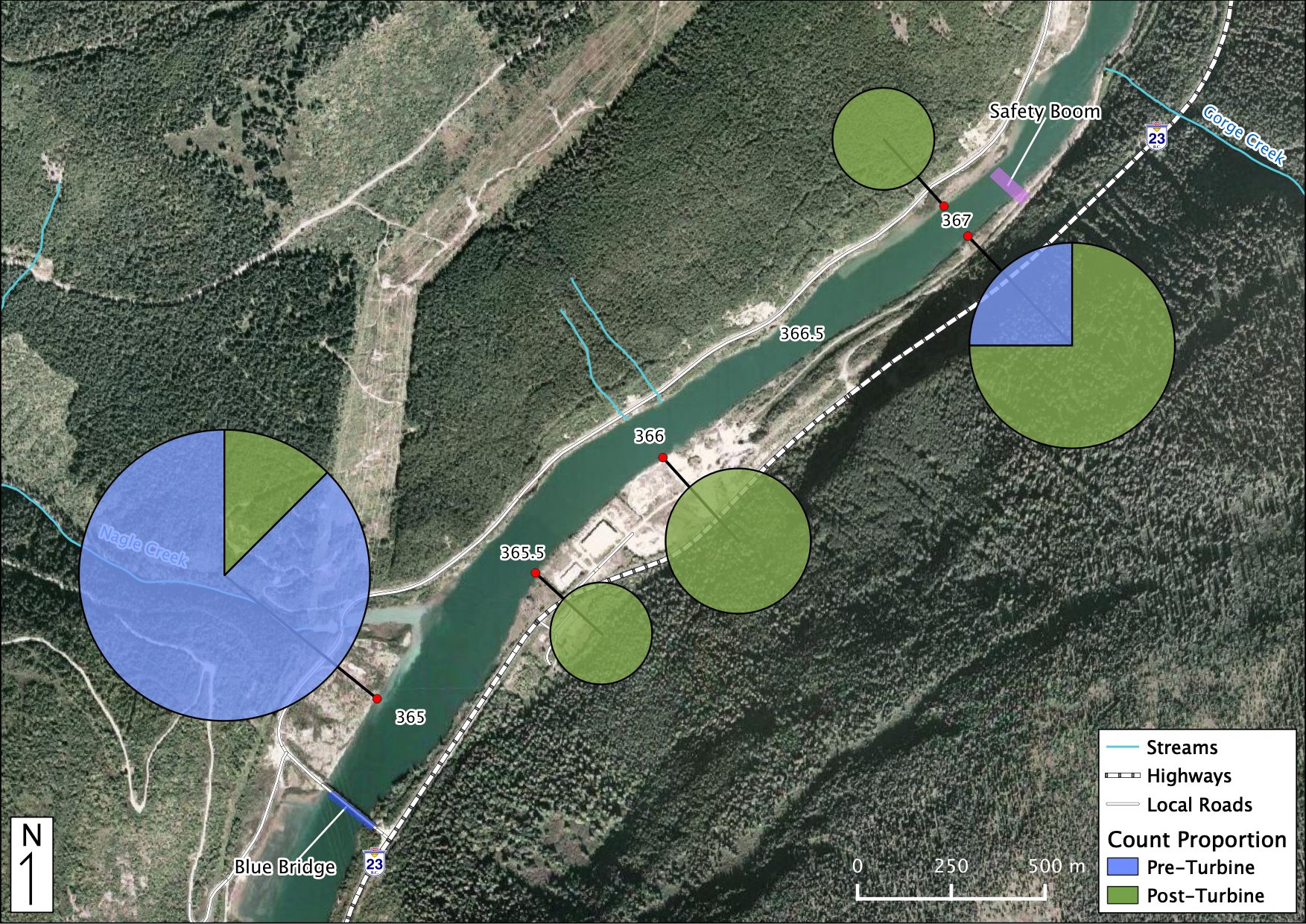
Figure 37. Relative Distribution of Fry Kokanee. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/ko-juv.png

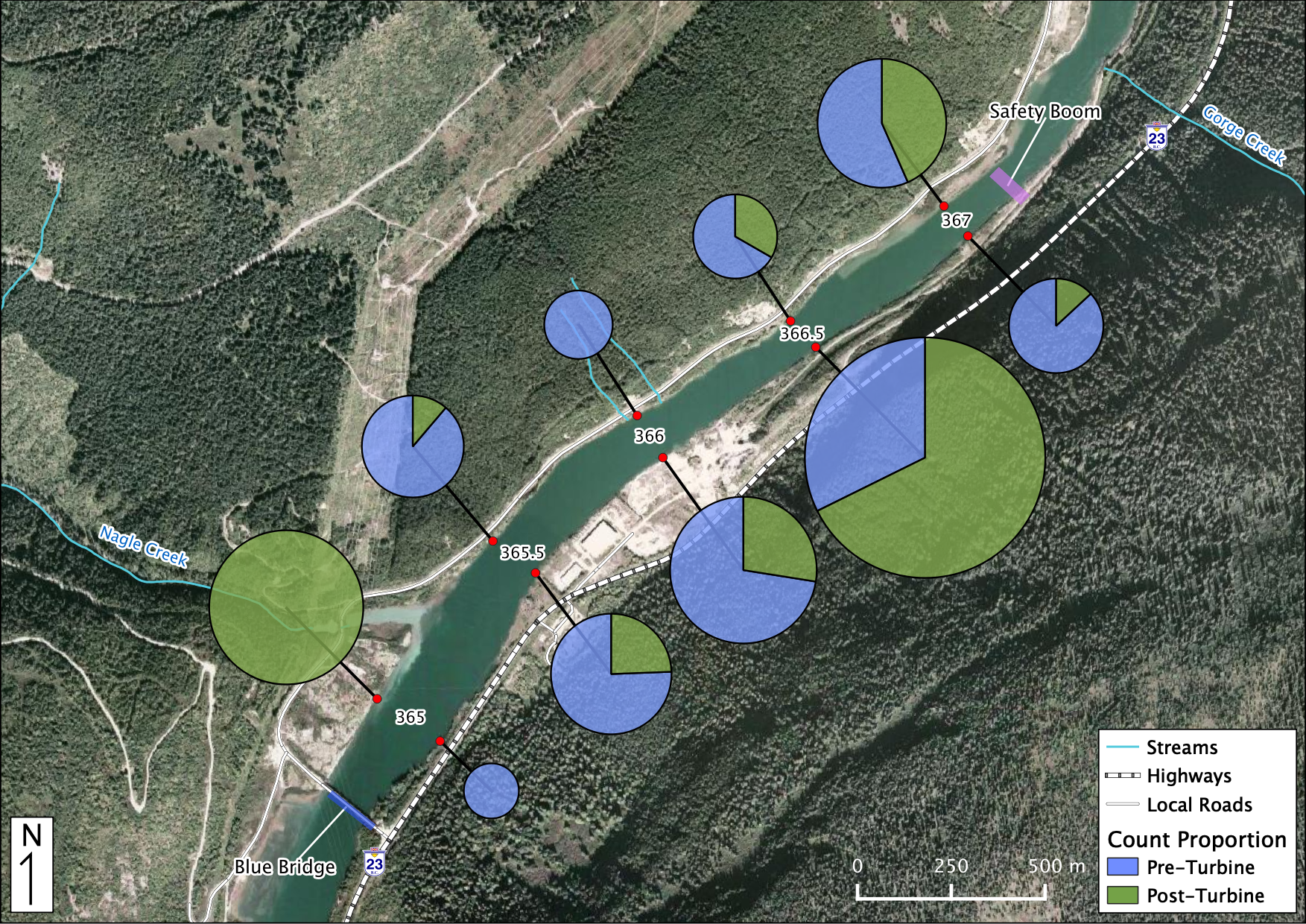
Figure 38. Relative Distribution of Juvenile Kokanee. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/mw-adult.png

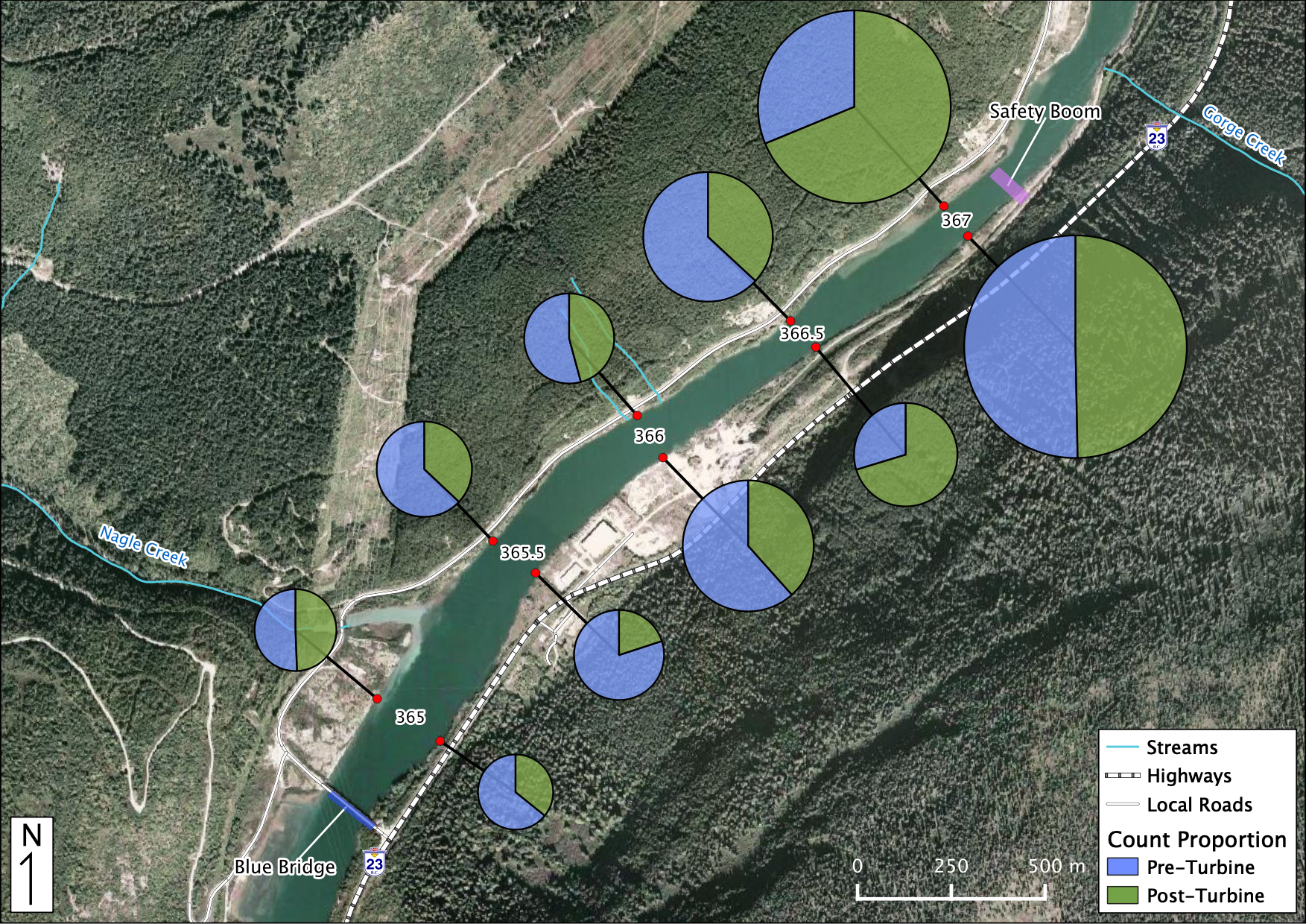
Figure 39. Relative Distribution of Adult Mountain Whitefish. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/mw-juv.png

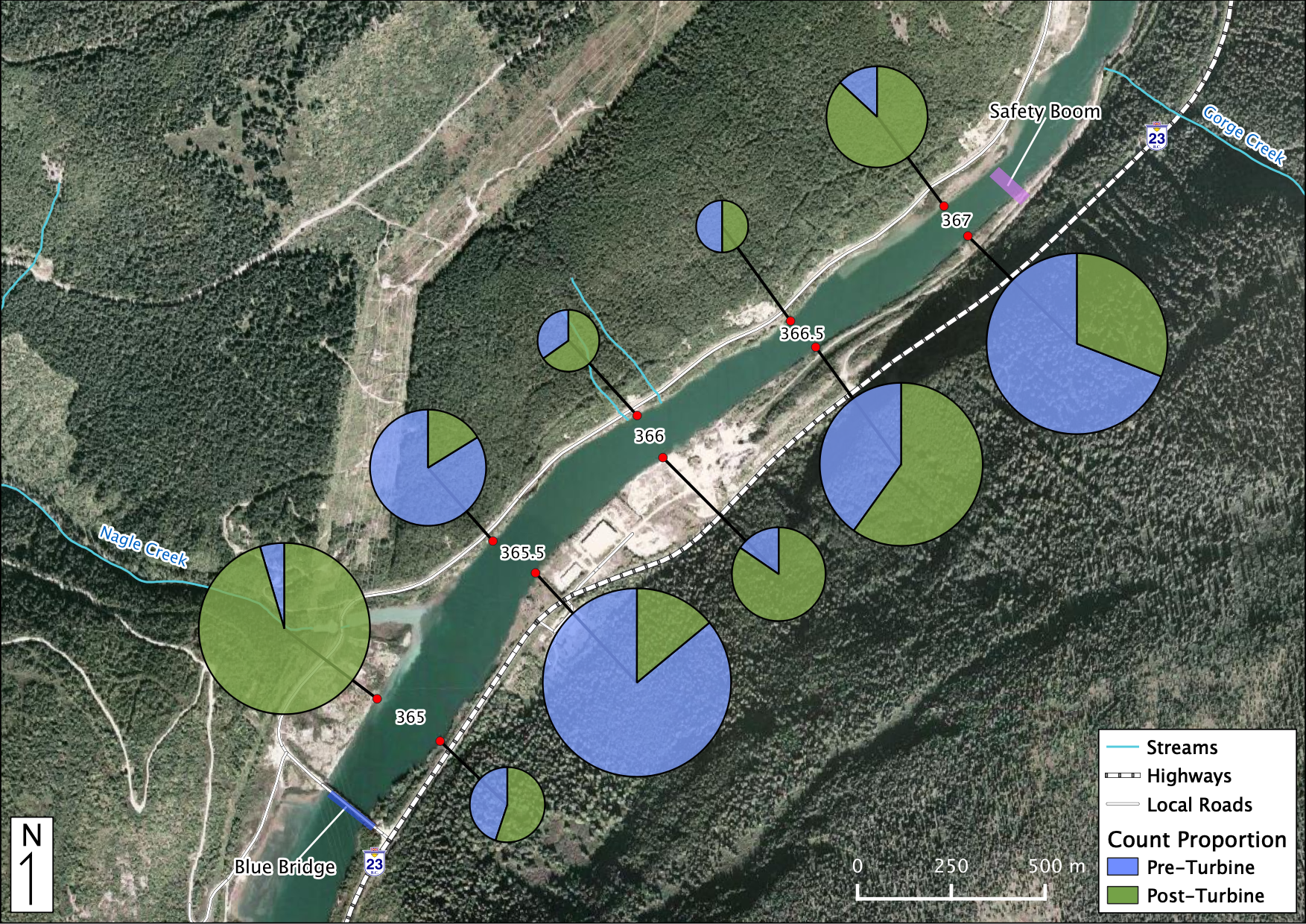
Figure 40. Relative Distribution of Juvenile Mountain Whitefish. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/rb-adult.png

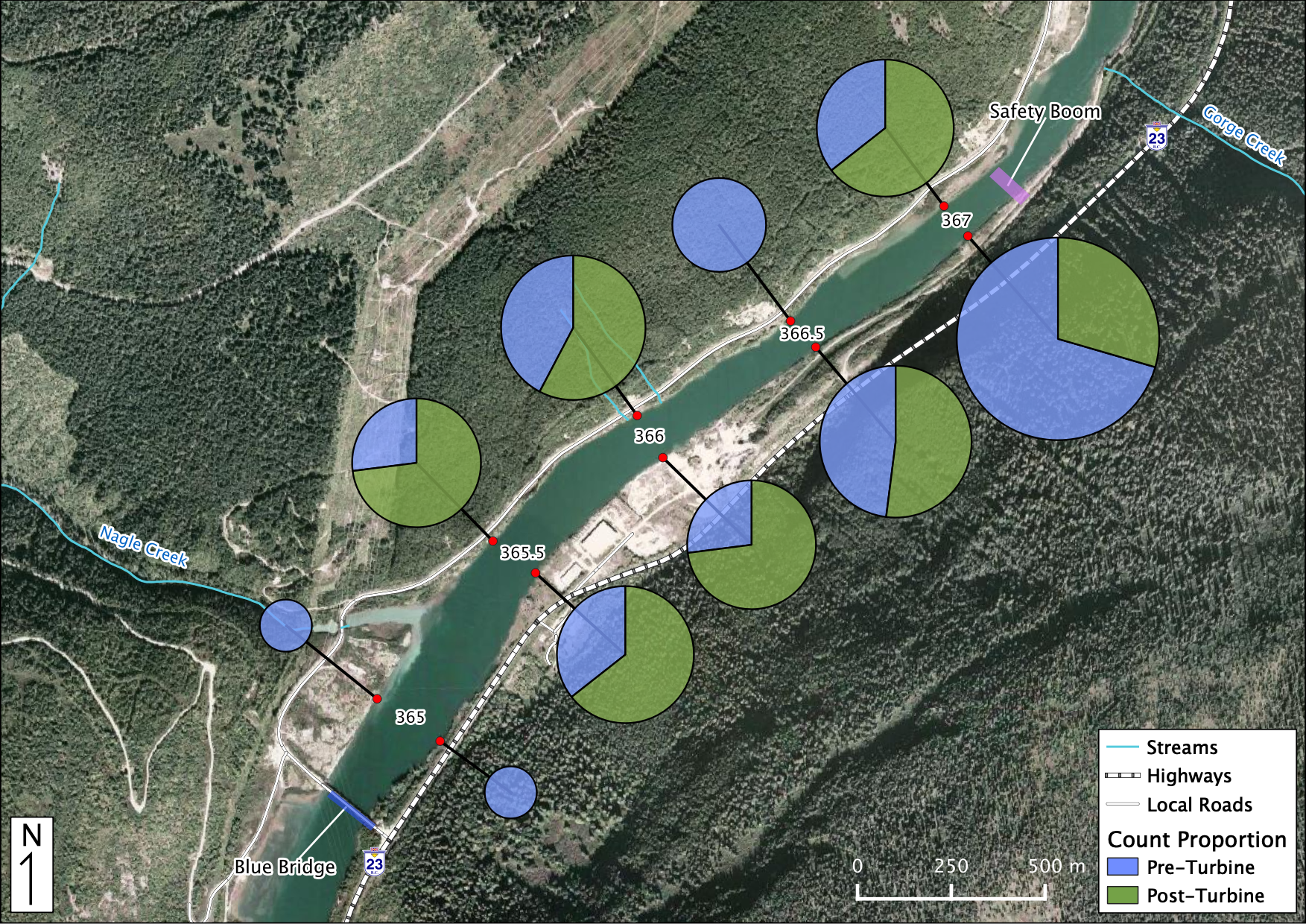
Figure 41. Relative Distribution of Adult Rainbow Trout. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

figures/map/relative-distribution/rb-juv.png

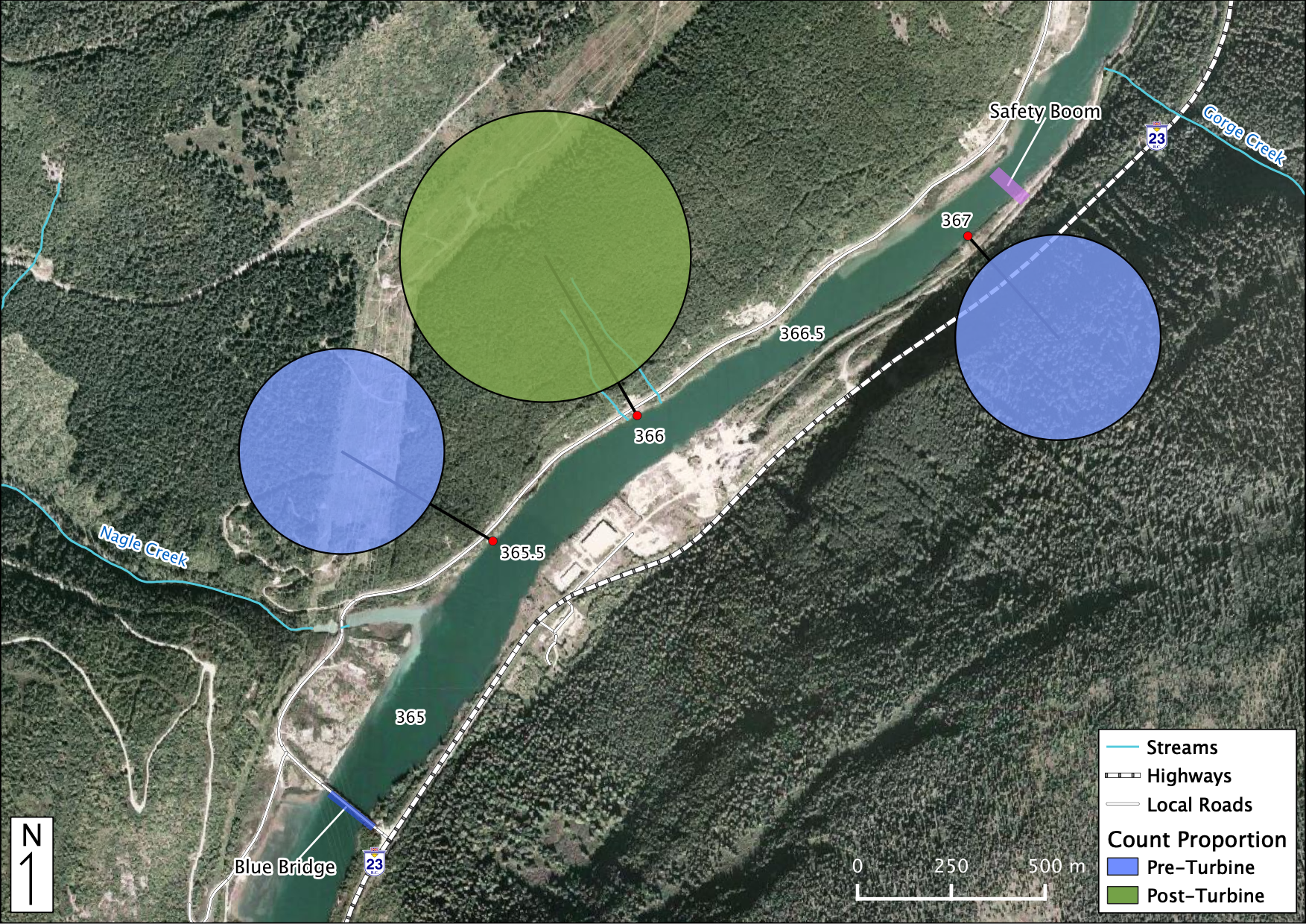
Figure 42. Relative Distribution of Juvenile Rainbow Trout. The sections in each piechart indicate the relative proportion of counts Pre vs Post-Turbine within that location while the size of each piechart indicates the distribution among locations.

Boat Counts

figures/map/raw-counts/all-bt.png

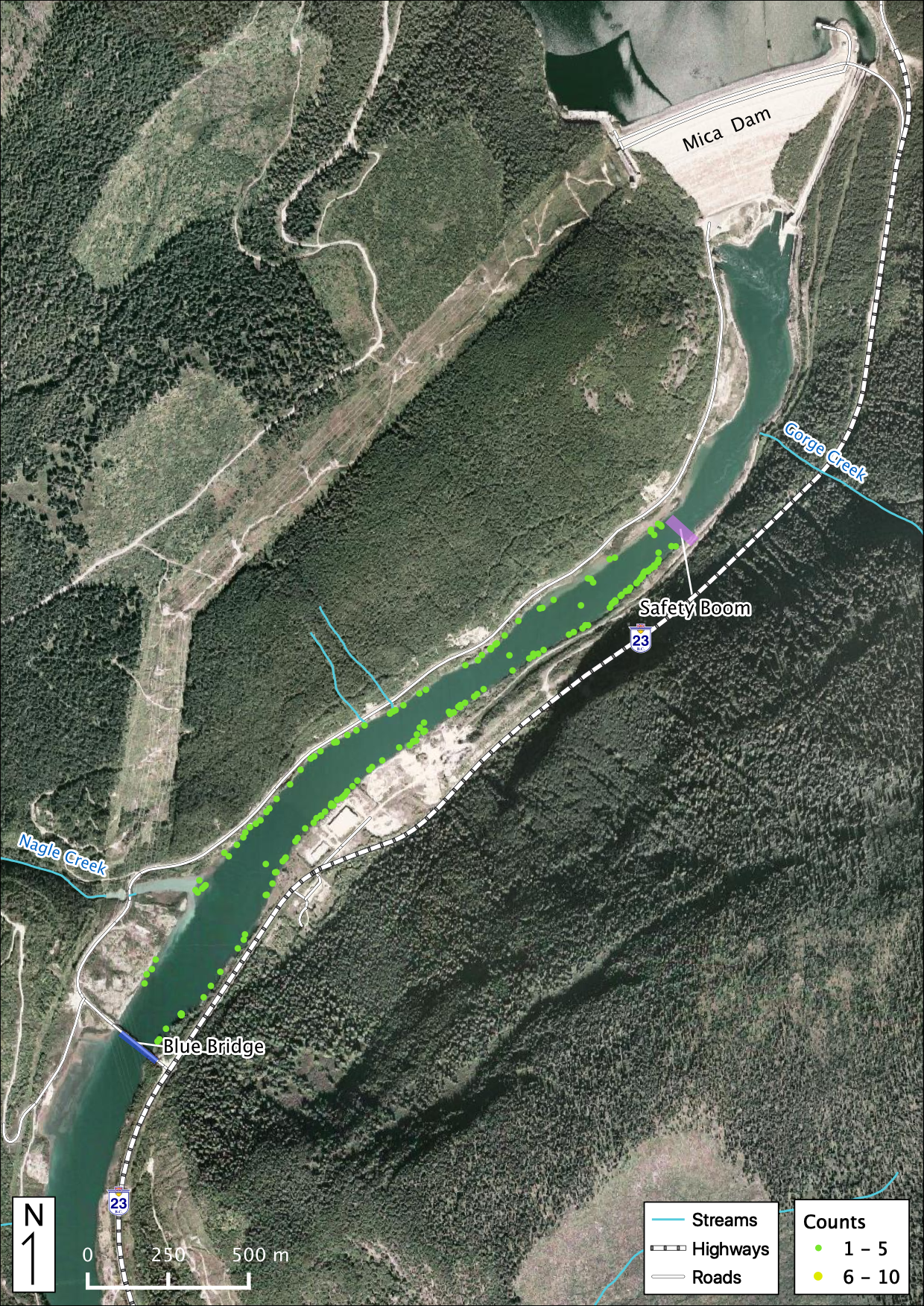
Figure 43. All Bull Trout observations in the study area below Mica Dam.

figures/map/raw-counts/all-ko.png

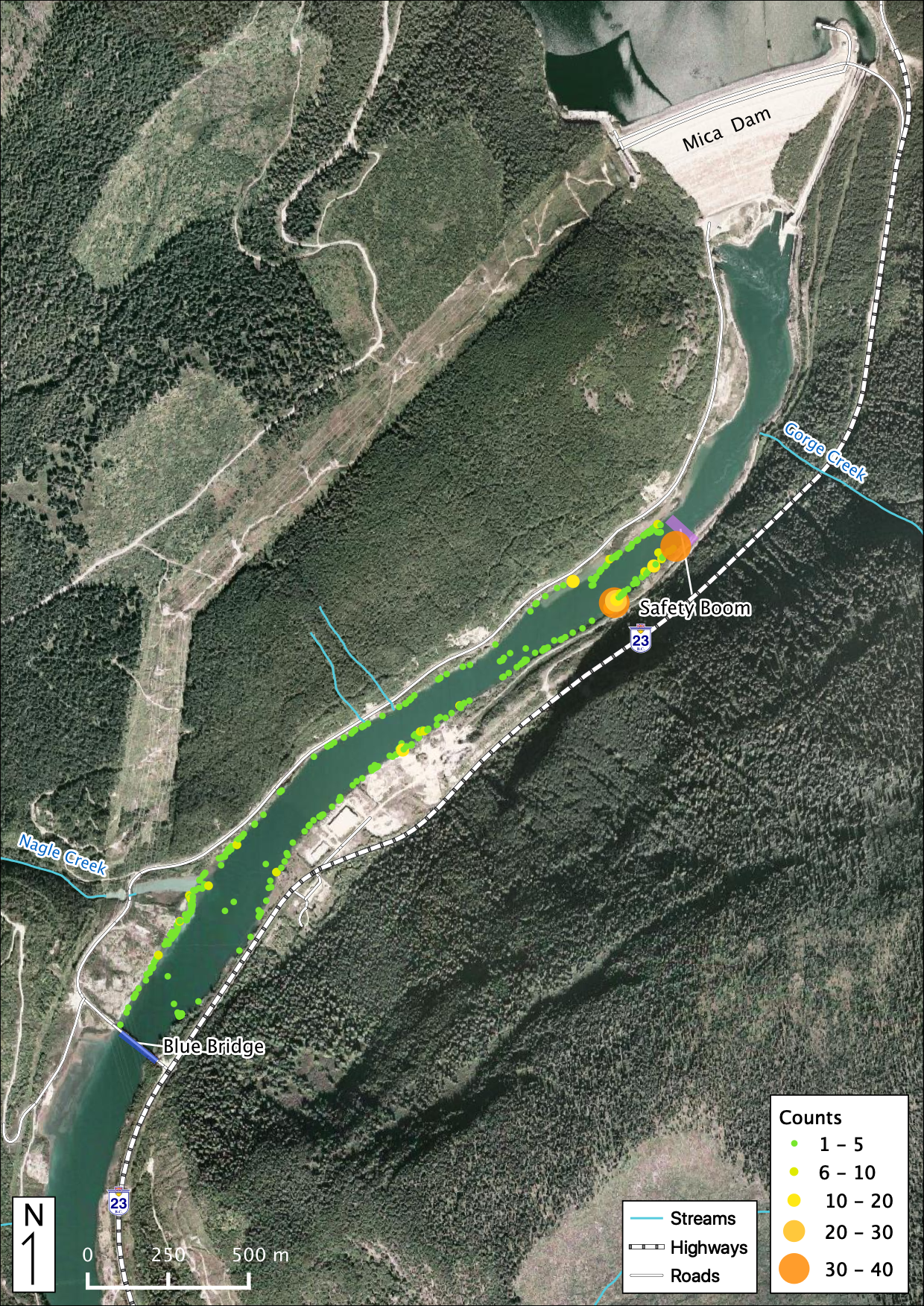
Figure 44. All Kokanee observations in the study area below Mica Dam.

figures/map/raw-counts/all-mw.png

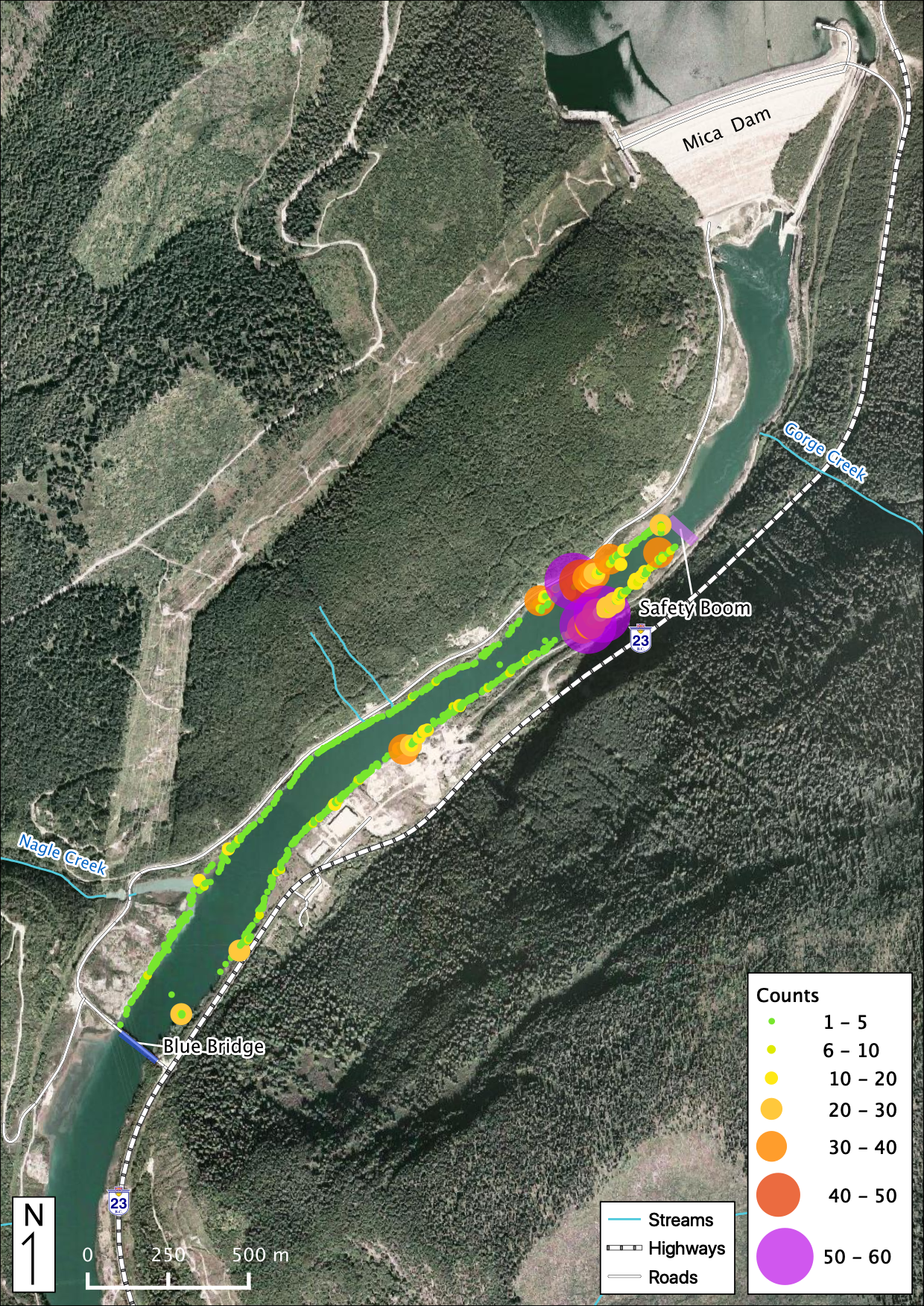
Figure 45. All Mountain Whitefish observations in the study area below Mica Dam.

figures/map/raw-counts/all-rb.png

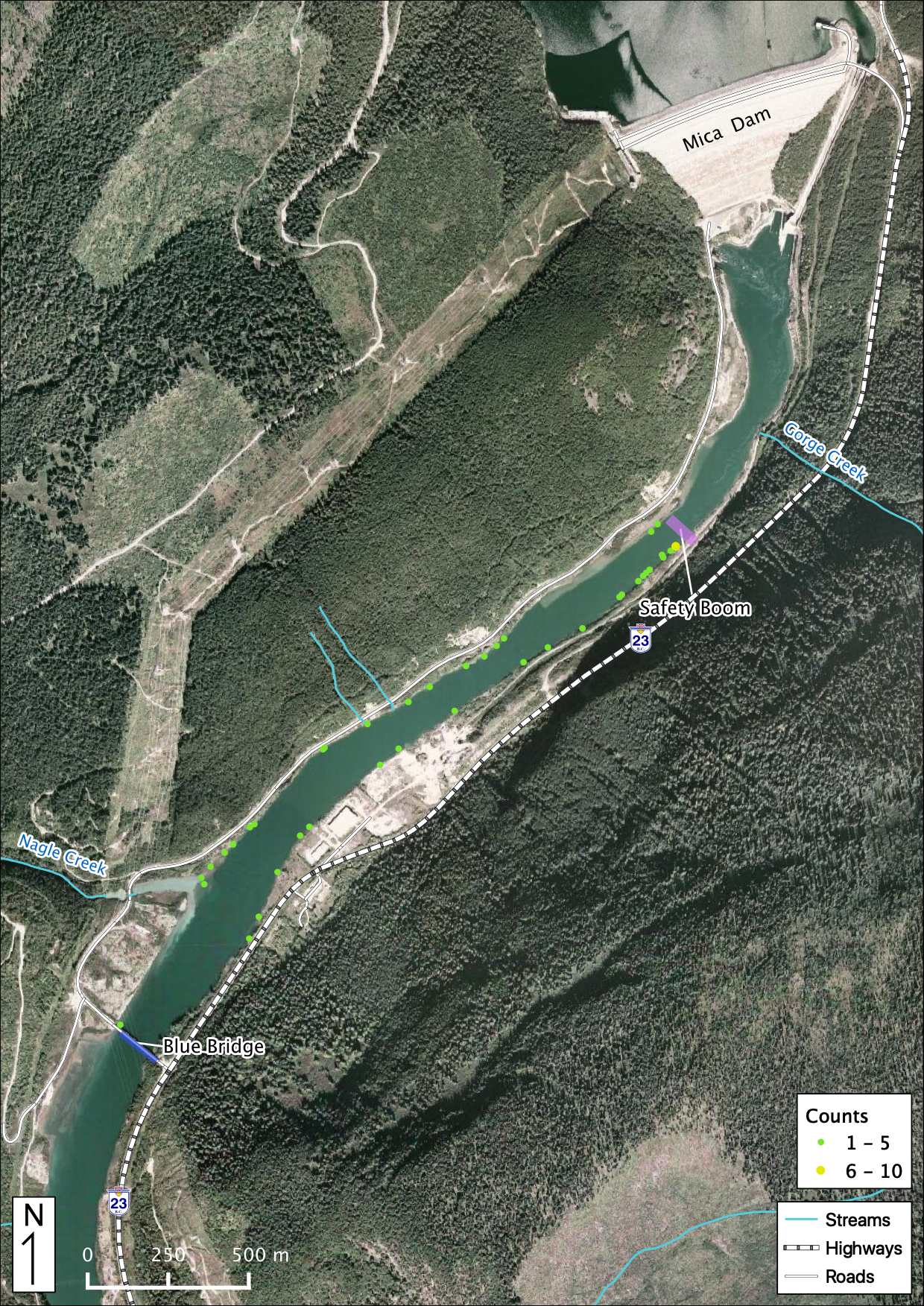
Figure 46. All Rainbow Trout observations in the study area below Mica Dam.

figures/map/raw-counts/bt-adult.png

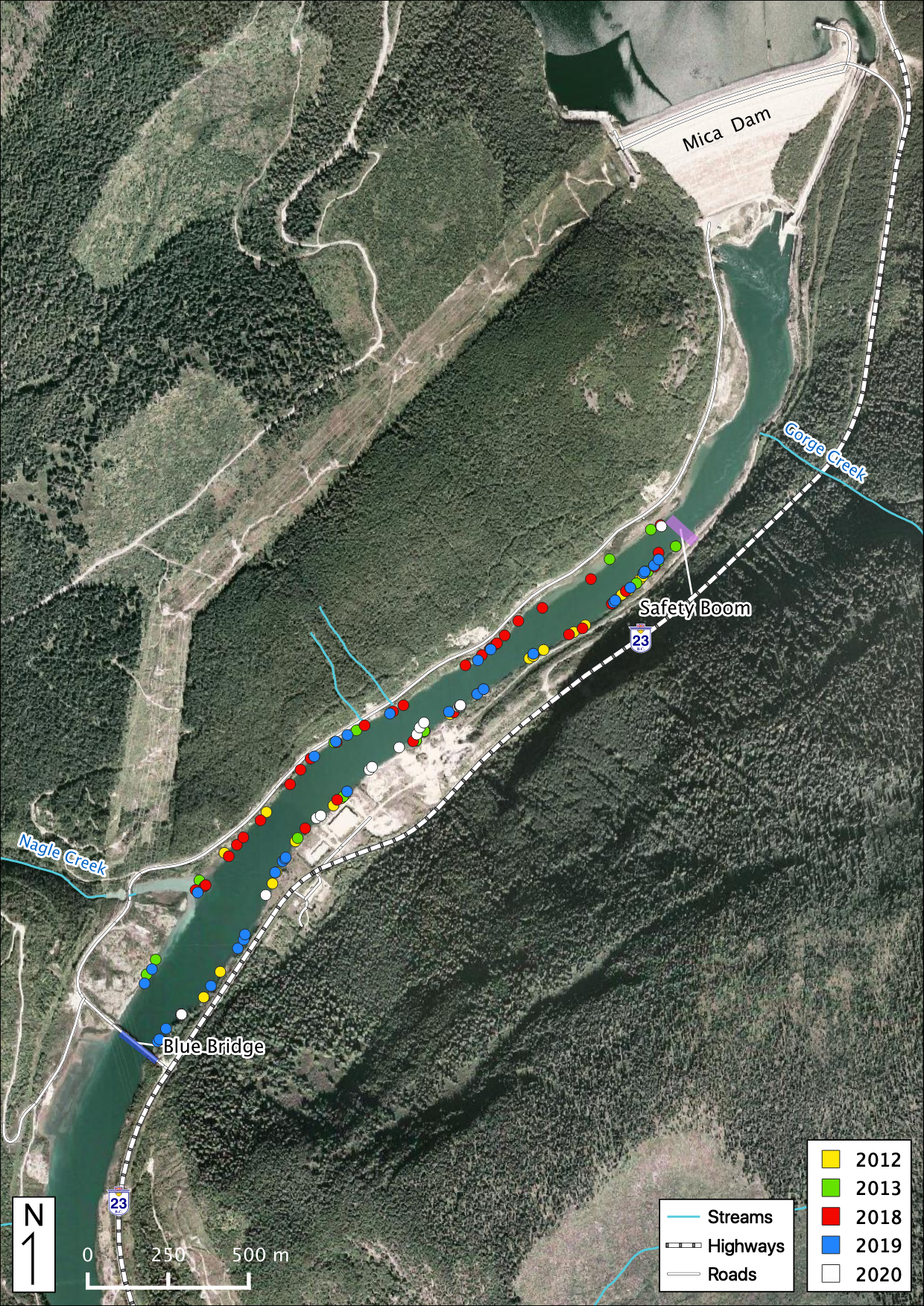
Figure 47. Adult Bull Trout observations in the study area below Mica Dam.

figures/map/raw-counts/bt-juv.png

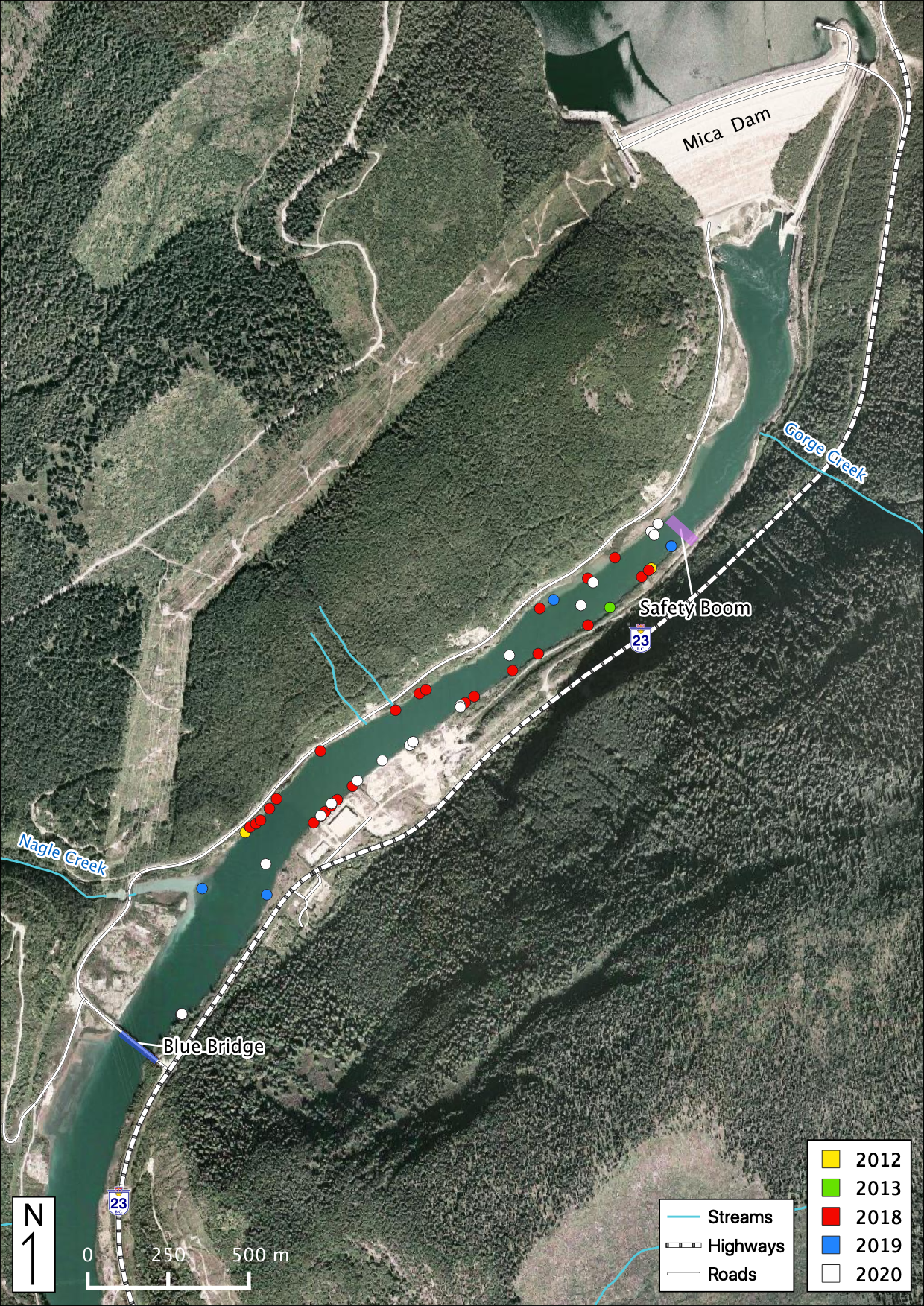
Figure 48. Juvenile Bull Trout observations in the study area below Mica Dam.

figures/map/raw-counts/ko-adult.png

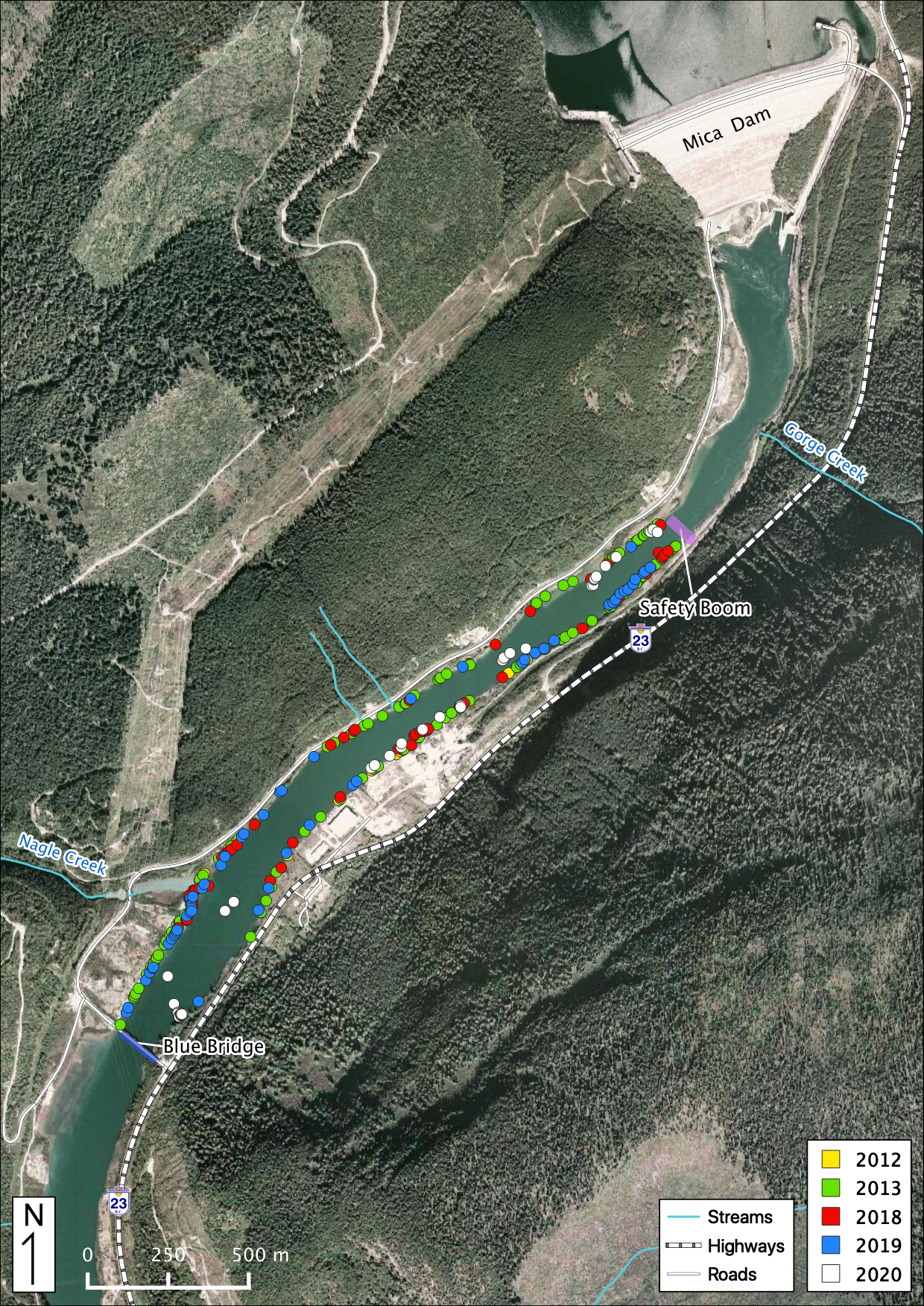
Figure 49. Adult Kokanee observations in the study area below Mica Dam.

figures/map/raw-counts/ko-juv-fry.png

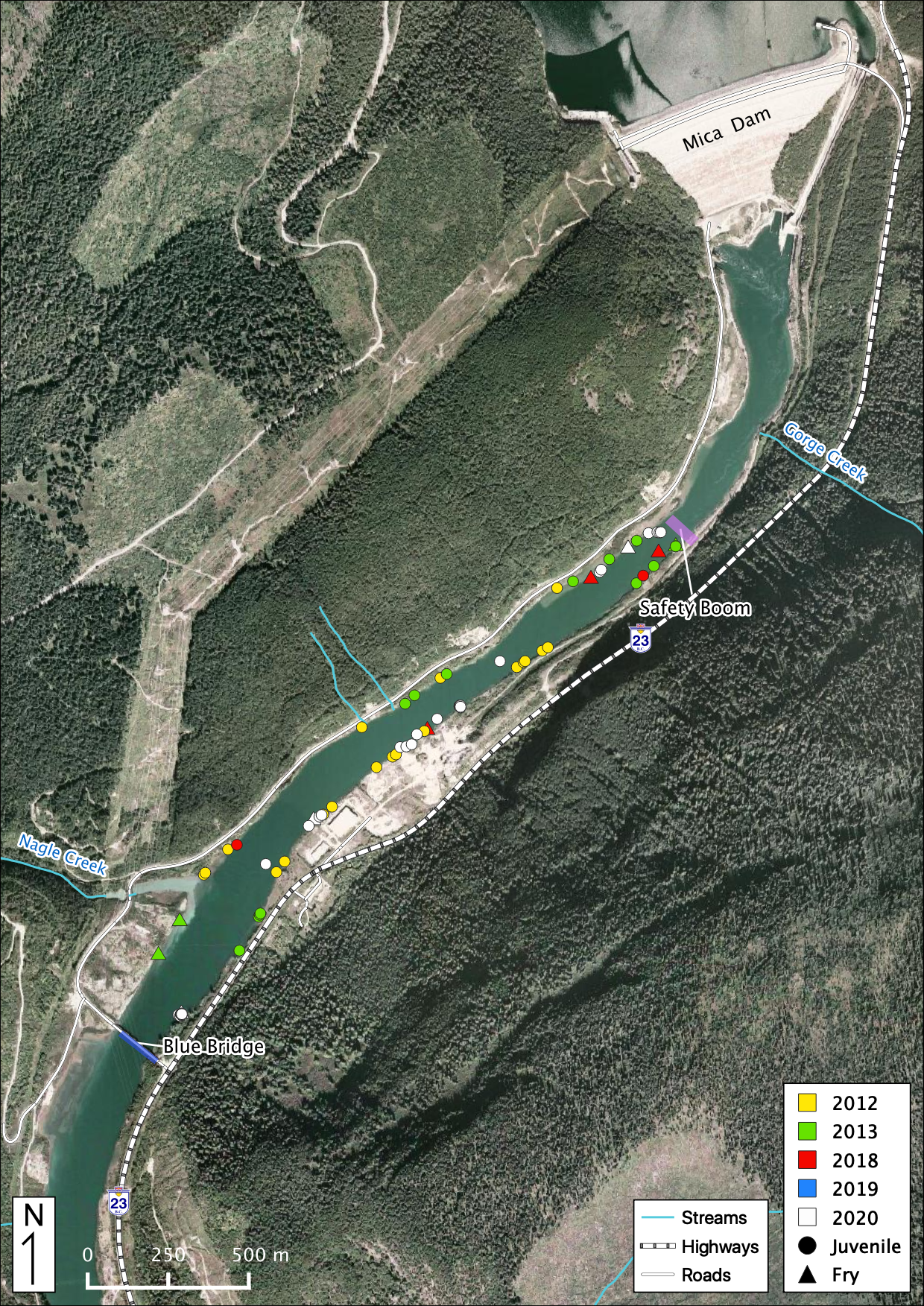
Figure 50. Juvenile and Fry Kokanee observations in the study area below Mica Dam.

figures/map/raw-counts/mw-adult.png

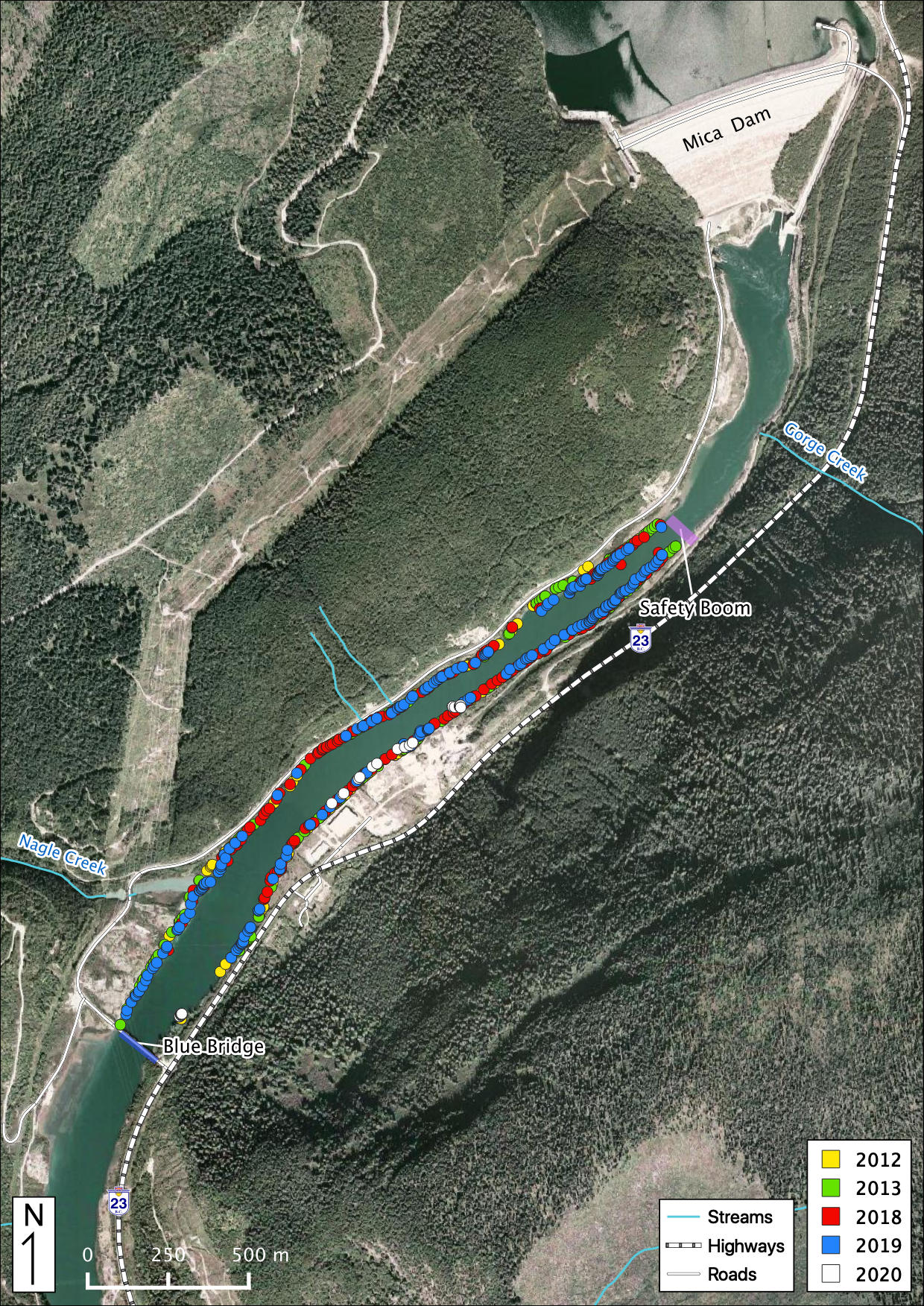
Figure 51. Adult Mountain Whitefish observations in the study area below Mica Dam.

figures/map/raw-counts/mw-juv-fry.png

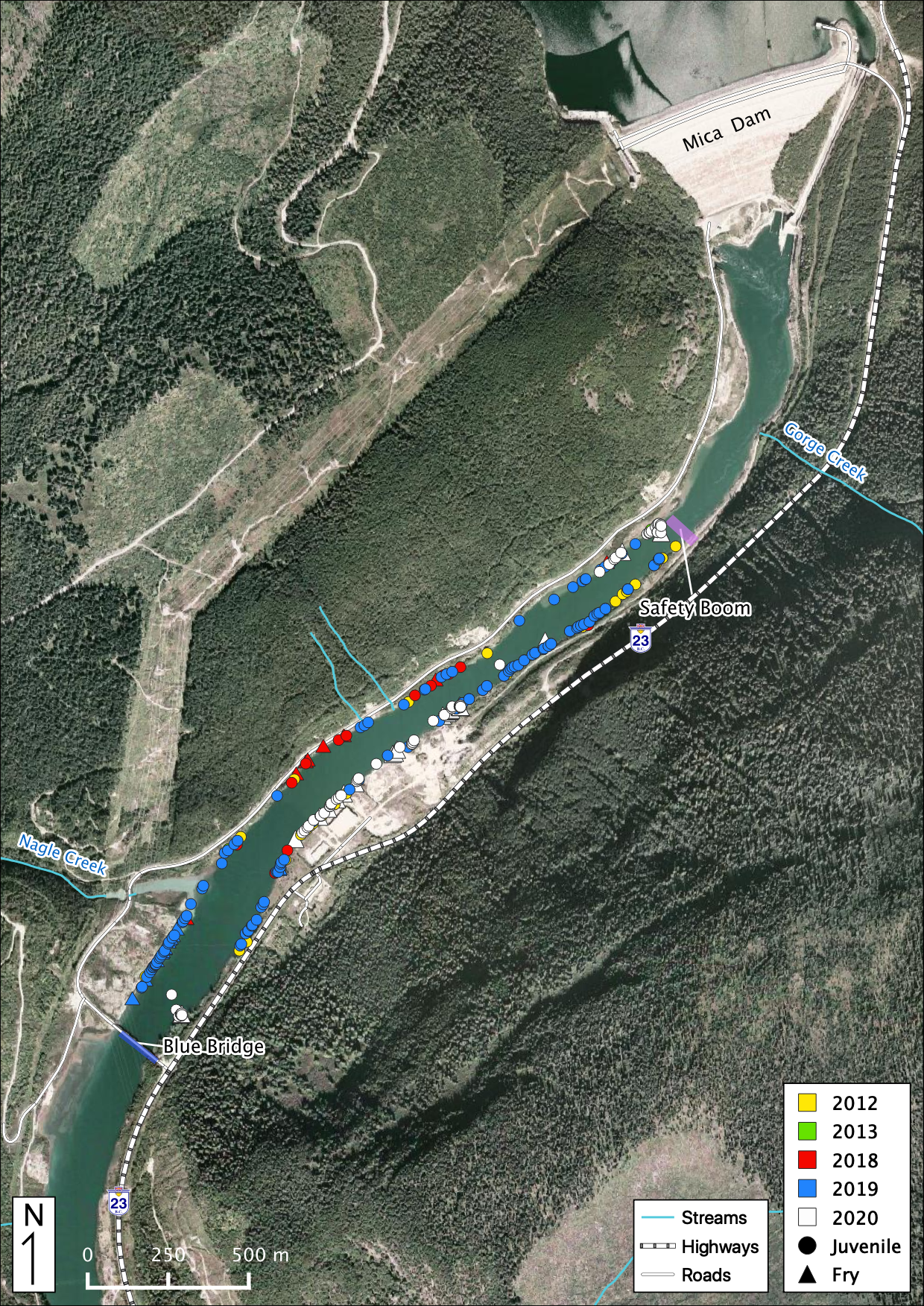
Figure 52. Juvenile and Fry Mountain Whitefish observations in the study area below Mica Dam.

figures/map/raw-counts/rb-adult.png

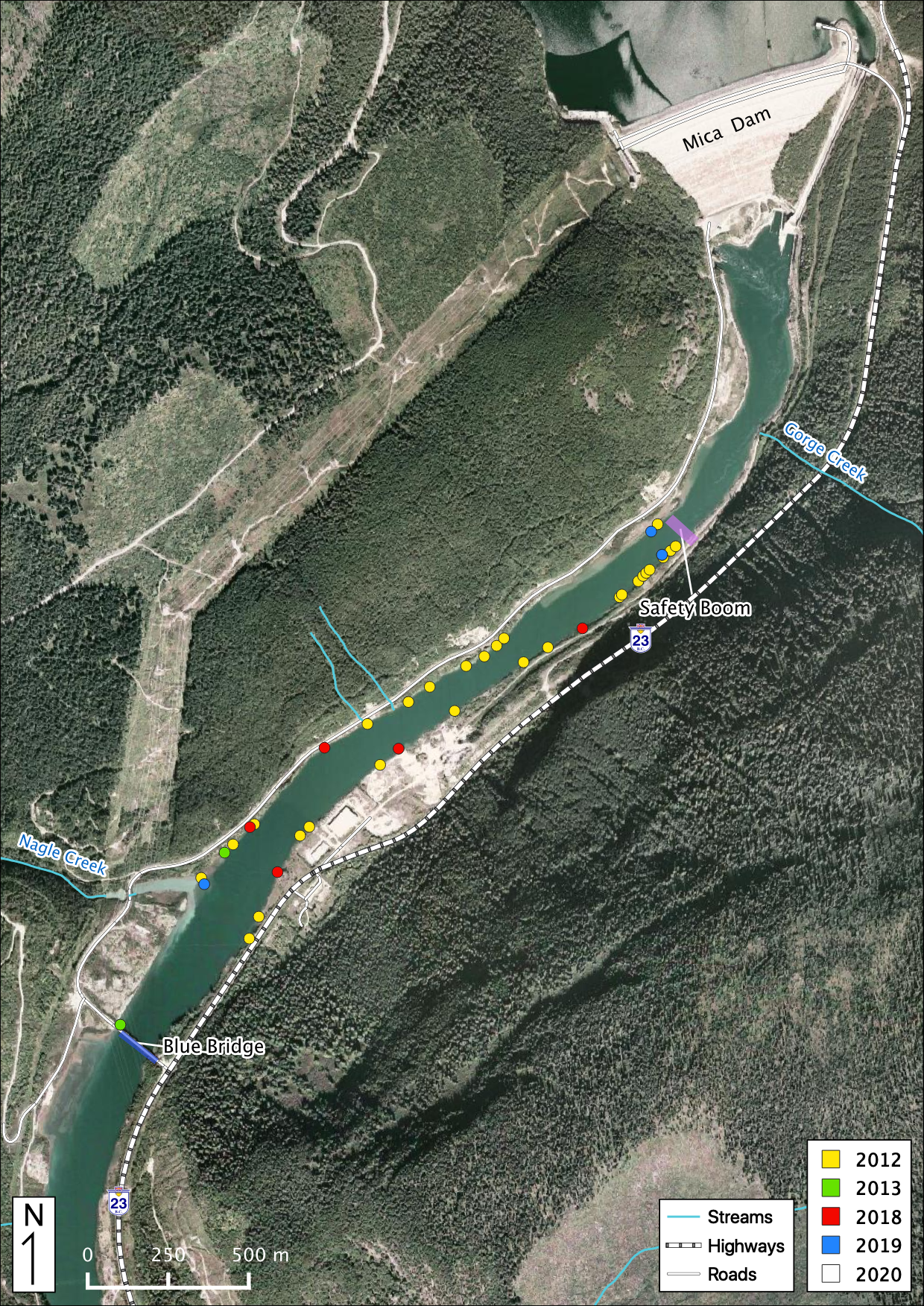
Figure 53. Adult Rainbow Trout observations in the study area below Mica Dam.

figures/map/raw-counts/rb-juv.png

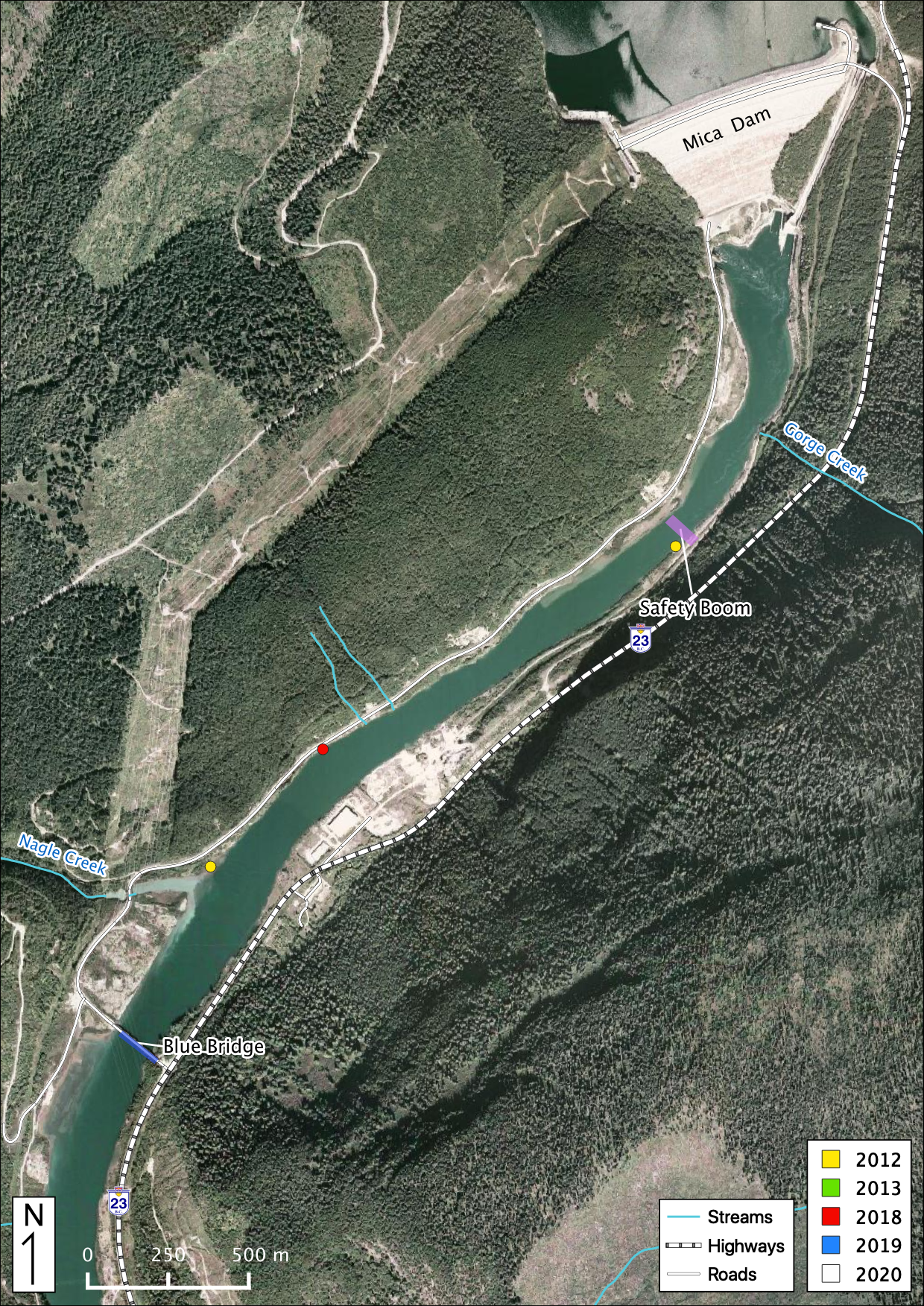
Figure 54. Juvenile Rainbow Trout observations in the study area below Mica Dam.

Acknowledgements

The organisations and individuals whose contributions have made this report possible include:

  • BC Hydro
    • Trish Joyce
    • Jason Watson
    • Margo Sadler
    • Guy Martel
    • Peter McCann
    • Fred Katunar
    • Alf Leake
    • Karen Bray
  • Ktunaxa Nation
    • Katrina Caley
    • Misun Kang
    • Joanne Fisher
    • Jim Clarricoates
    • Bill Green
  • Poisson Consulting
    • Robyn Irvine
    • Seb Dalgarno
  • Applied Aquatic Research
    • Tom Boag
  • Ministry of Forests, Lands and Natural Resource Operations
    • Albert Chirico
    • Will Warnock
  • Jon Bisset
  • Mark Thomas
  • Charlotte Houston

References

Bradford, Michael J, Josh Korman, and Paul S Higgins. 2005. “Using Confidence Intervals to Estimate the Response of Salmon Populations (Oncorhynchus Spp.) To Experimental Habitat Alterations.” Canadian Journal of Fisheries and Aquatic Sciences 62 (12): 2716–26. https://doi.org/10.1139/f05-179.
Brooks, Steve, Andrew Gelman, Galin L. Jones, and Xiao-Li Meng, eds. 2011. Handbook for Markov Chain Monte Carlo. Boca Raton: Taylor & Francis.
Gelman, Andrew, Daniel Simpson, and Michael Betancourt. 2017. “The Prior Can Often Only Be Understood in the Context of the Likelihood.” Entropy 19 (10): 555. https://doi.org/10.3390/e19100555.
Greenland, Sander. 2019. “Valid p -Values Behave Exactly as They Should: Some Misleading Criticisms of p -Values and Their Resolution With s -Values.” The American Statistician 73 (sup1): 106–14. https://doi.org/10.1080/00031305.2018.1529625.
Greenland, Sander, and Charles Poole. 2013. “Living with p Values: Resurrecting a Bayesian Perspective on Frequentist Statistics.” Epidemiology 24 (1): 62–68. https://doi.org/10.1097/EDE.0b013e3182785741.
He, Ji X., James R. Bence, James E. Johnson, David F. Clapp, and Mark P. Ebener. 2008. “Modeling Variation in Mass-Length Relations and Condition Indices of Lake Trout and Chinook Salmon in Lake Huron: A Hierarchical Bayesian Approach.” Transactions of the American Fisheries Society 137 (3): 801–17. https://doi.org/10.1577/T07-012.1.
Kery, Marc, and Michael Schaub. 2011. Bayesian Population Analysis Using WinBUGS : A Hierarchical Perspective. Boston: Academic Press. http://www.vogelwarte.ch/bpa.html.
Kristensen, Kasper, Anders Nielsen, Casper W. Berg, Hans Skaug, and Bradley M. Bell. 2016. “TMB : Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software 70 (5). https://doi.org/10.18637/jss.v070.i05.
McElreath, Richard. 2016. Statistical Rethinking: A Bayesian Course with Examples in R and Stan. Chapman & Hall/CRC Texts in Statistical Science Series 122. Boca Raton: CRC Press/Taylor & Francis Group.
Millar, R. B. 2011. Maximum Likelihood Estimation and Inference: With Examples in R, SAS, and ADMB. Statistics in Practice. Chichester, West Sussex: Wiley.
Plummer, Martyn. 2003. “JAGS: A Program for Analysis of Bayesian Graphical Models Using Gibbs Sampling.” In Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003), edited by Kurt Hornik, Friedrich Leisch, and Achim Zeileis. Vienna, Austria.
R Core Team. 2020. “R: A Language and Environment for Statistical Computing.” Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Columbia River Mica Dam Bull Trout Kokanee Mountain Whitefish Rainbow Trout Sculpin Growth Condition Water Temperature